Control Estadístico de Calidad
SOLUCIÓN TALLER #1
Exercises Introduction to Statistical Quality Control Montgomery
5.6
El peso neto (en onzas) de un producto de blanqueador seco debe ser monitoreado mediante las cartas de control \(\overline{X}\) y \(R\) utilizando un tamaño de muestra de \(n=5\). Los datos de \(20\) muestras preliminares son los siguientes.
- a). Realice las cartas de control \(\overline{X}\) y \(R\) usando estos datos. ¿El proceso exhibe control estadístico?
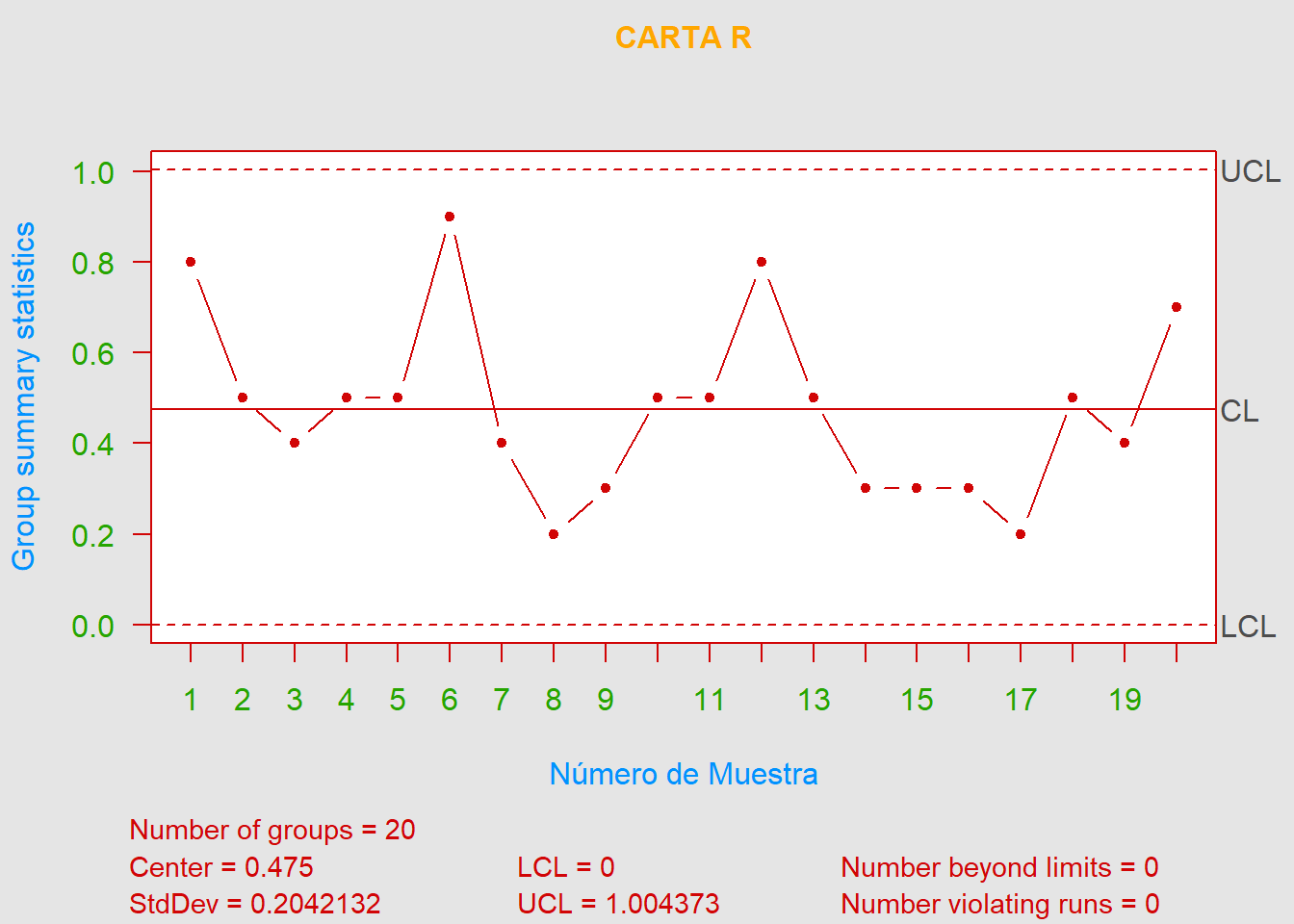
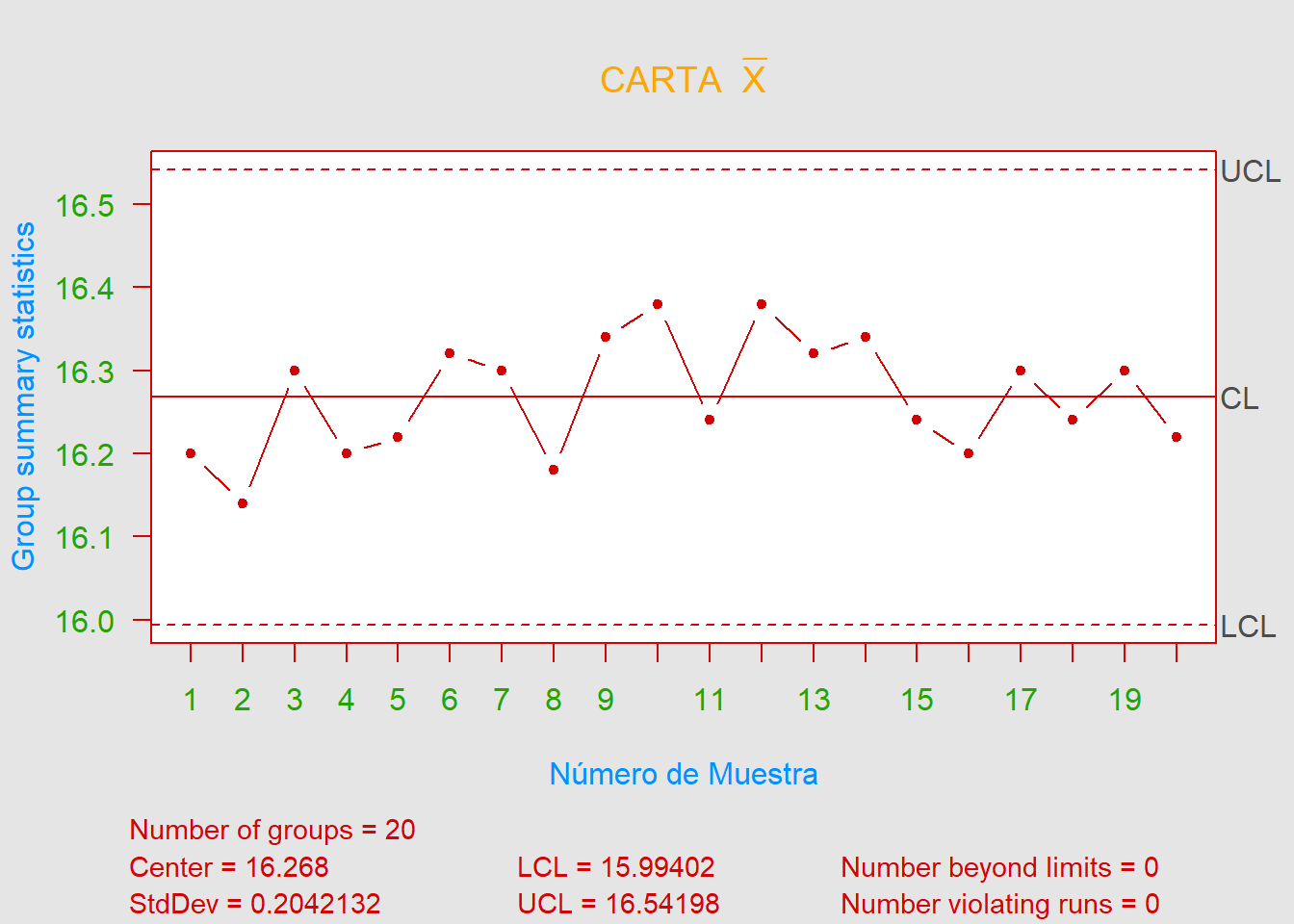
De acuerdo con las cartas de control \(R\) y \(\overline{X}\) podemos afirmar que el proceso está bajo control estadístico.
- b). Estime la media y la desviación estándar del proceso.
\[\widehat{\mu} = LC_{\overline{x}} = \color{red} {16.268} \hspace{0.5cm}\text{y}\hspace{0.5cm} \widehat{\sigma} = \frac{\overline{R}}{d_2} = \frac{0.475}{2.326} = \color{blue} {0.2042132}\]
- c). ¿Parece que el peso de relleno sigue una distribución normal?
soloNumeros <- c(Data$x1, Data$x2, Data$x3, Data$x4, Data$x5)
shapiro.test(soloNumeros) # Prueba de Shapiro-Wilk##
## Shapiro-Wilk normality test
##
## data: soloNumeros
## W = 0.96818, p-value = 0.01608tseries::jarque.bera.test(soloNumeros) # Prueba Jarque-Bera##
## Jarque Bera Test
##
## data: soloNumeros
## X-squared = 1.433, df = 2, p-value = 0.4885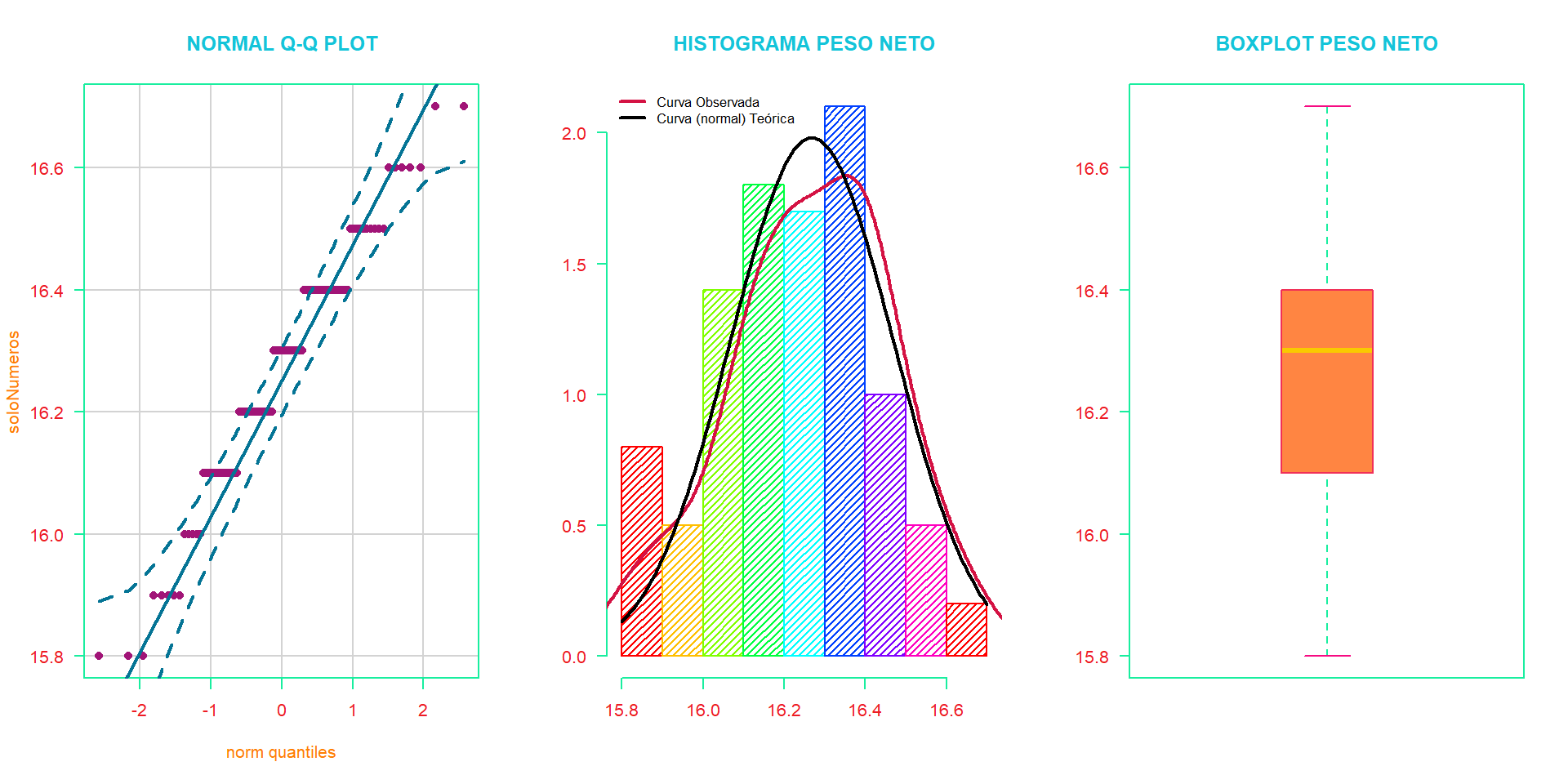
En este caso como el tamaño de muestra no es muy grande (\(n=100\)) no se recomienda usar la prueba de Kolmogorov-Smirnov, usaremos entonces las que se ajusten mejor a nuestro caso. Tanto el test de Shapiro-Wilk como el de Jarque-Bera nos indican que los datos provienen de una distribución normal, ya que el p-valor \(\color{green} {>} \alpha\) por lo tanto no se rechaza \(H_0 :=\) Los datos siguen una distribución normal. Finalmente, podemos afirmar que, con un nivel de confianza del \(90\%\), el peso de relleno sigue una distribución normal y gráficamente pareciese ser así.
- d). Si las especificaciones están en \(16.2 \pm 0.5\), ¿qué conclusiones sacaría sobre la capacidad del proceso?
\[\widehat{C}_p = \frac{\text{LES}-\text{LEI}}{6\widehat{\sigma}} = \frac{16.7-15.7}{6 \cdot 0.2042} = \color{orange} {0.816}\]
Por lo tanto, el proceso no es capaz de cumplir con las especificaciones.
- e). ¿Qué fracción de envases producidos por este proceso es probable que esté por debajo del límite inferior de especificación de \(15.7\) oz?
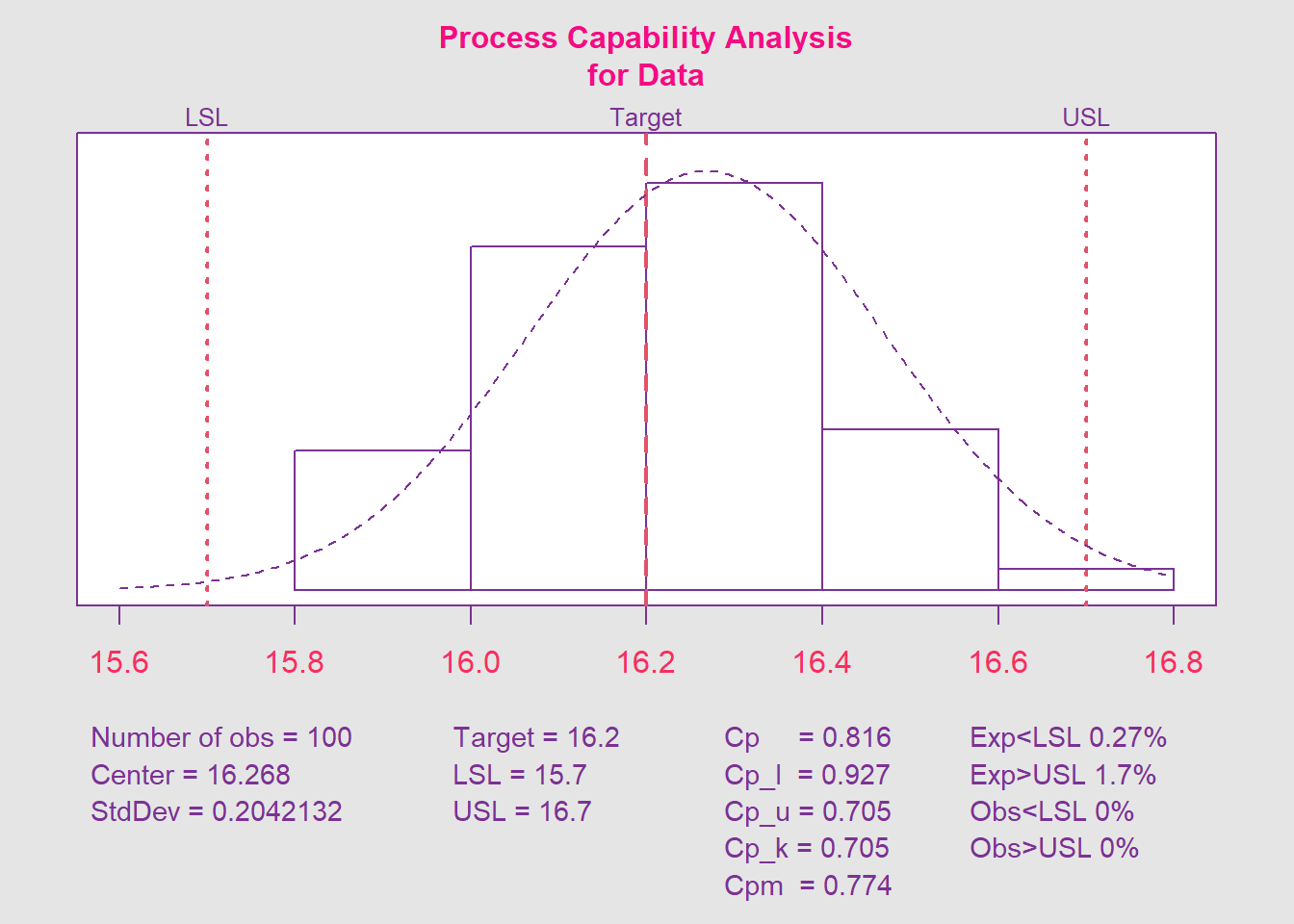
\[\textrm{P}(X<\text{LEI}) = \textrm{P}(X<15.7) = \textrm{P}\left( Z<\frac{15.7-16.268}{0.2042} \right) = \Phi(-2.782) = \color{green} {0.0027}\]
De acuerdo con lo anterior, \(\approx 3\) de cada \(1000\) envases producidos por el proceso está por debajo del límite inferior de especificación.
5.10
Se toman muestras de \(n=8\) artículos de un proceso de fabricación a intervalos regulares. Se mide una característica de calidad y se calculan los valores \(\overline{x}\) y \(R\) para cada muestra. Después de 50 muestras, tenemos.
\[\sum_{i=1}^{50} \overline{x}_i = 2000 \hspace{0.5cm}\text{y}\hspace{0.5cm} \sum_{i=1}^{50} R_i = 250\]
Suponga que la característica de calidad se distribuye normal.
- a). Calcule los límites de control para las cartas \(\overline{X}\) y \(R\).
\[\begin{align*} \overline{\overline{X}} &= \frac{\sum_{i=1}^{50}\overline{x}_i}{m} = \frac{2000}{50} = 40 \\ \overline{R} &= \frac{\sum_{i=1}^{50}R_i}{m} = \frac{250}{50} = 5 \end{align*}\]
Límites para la carta \(\overline{X}\), \[\begin{align*} \text{LCS} &= \overline{\overline{X}}+A_2\overline{R} = 40+(0.373\cdot 5) = \color{red} {41.865} \\ \text{LC} &= \overline{\overline{X}} = \color{green} {40} \\ \text{LCI} &= \overline{\overline{X}}+A_2\overline{R} = 40-(0.373\cdot 5) = \color{blue} {38.135} \end{align*}\]
Límites para la carta \(R\), \[\begin{align*} \text{LCS} &= \overline{R}D_4 = 5\cdot 1.864 = \color{red} {9.32} \\ \text{LC} &= \overline{R} = \color{orange} {5} \\ \text{LCI} &= \overline{R}D_3 = 5\cdot 0.136 = \color{blue} {0.68} \end{align*}\]
- c). Si los límites de la especificación son \(41 \pm 5.0\), ¿cuáles son sus conclusiones con respecto a la capacidad del proceso para producir artículos dentro de estas especificaciones?
\[\widehat{\sigma}_x = \frac{\overline{R}}{d_2} = \frac{5}{2.847} = \color{magenta} {1.756235}\] \[\widehat{C}_p = \frac{\text{LES}-\text{LEI}}{6\widehat{\sigma}} = \frac{46-36}{6\cdot 1.7562} = \color{purple} {0.949}\]
Se considera que un valor mayor o igual a \(1\) es señal de una buena capacidad.
- d). Suponiendo que, si un artículo excede el límite superior de la especificación, se puede volver a trabajar, y si está por debajo del límite inferior de la especificación, se debe desechar, ¿qué porcentaje de rechazo y retrabajo está produciendo el proceso?
\[\begin{align*} \textrm{P}(\color{green} {rehacer}) &= \textrm{P}(X>\text{LES}) = 1-\Phi\left( \frac{46-40}{1.756} \right) = 1-\Phi(3.4164) =\color{green} {0.00032} \\ \textrm{P}(\color{red} {desechar}) &= \textrm{P}(X<\text{LEI}) = \Phi\left( \frac{36-40}{1.756} \right) = \Phi(-2.2776) = \color{red} {0.01138} \end{align*}\]
Por lo tanto, el \(0.032\%\) de los artículos se pueden volver a trabajar (rehacer) y el \(1.138\%\) de los artículos se deben desechar.
- e). Haga sugerencias sobre cómo se podría mejorar el rendimiento del proceso.
Una recomendación para mejorar el desempeño del proceso sería revisar éste para ver si es posible disminuir la variabilidad, aumentar la media del proceso puede que no sea correcto, ya que es posible que por especificaciones de ingeniería no deba aumentar la media.
5.13
Las piezas fabricadas mediante un proceso de moldeo por inyección se someten a una prueba de resistencia a la compresión. Se recogen veinte muestras de cinco partes cada una, y las resistencias a la compresión (en psi) se muestran en la siguiente tabla.
- a). Establezca gráficos de control \(\overline{X}\) y \(R\) para la resistencia a la compresión utilizando estos datos. ¿Está el proceso en control estadístico?
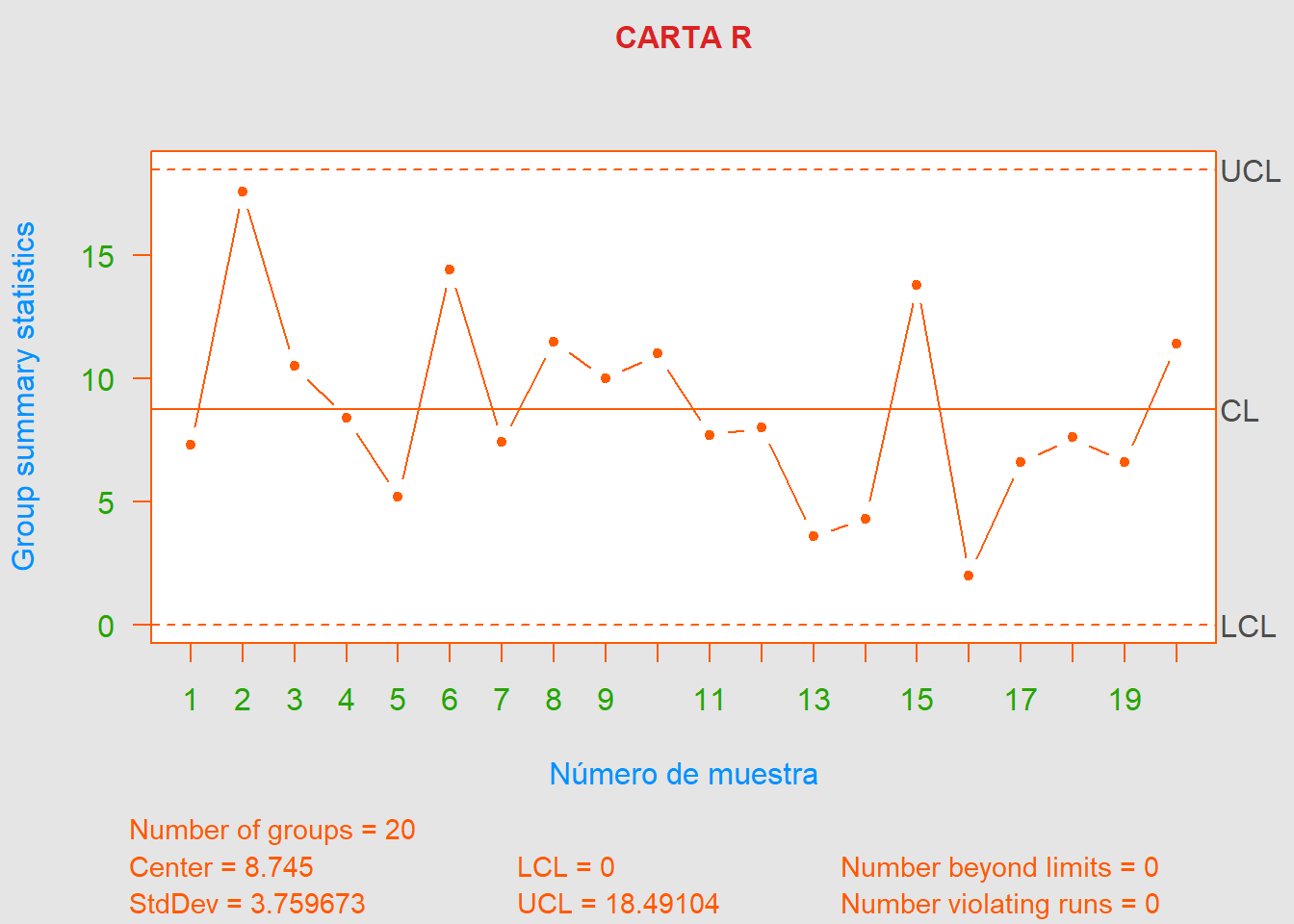
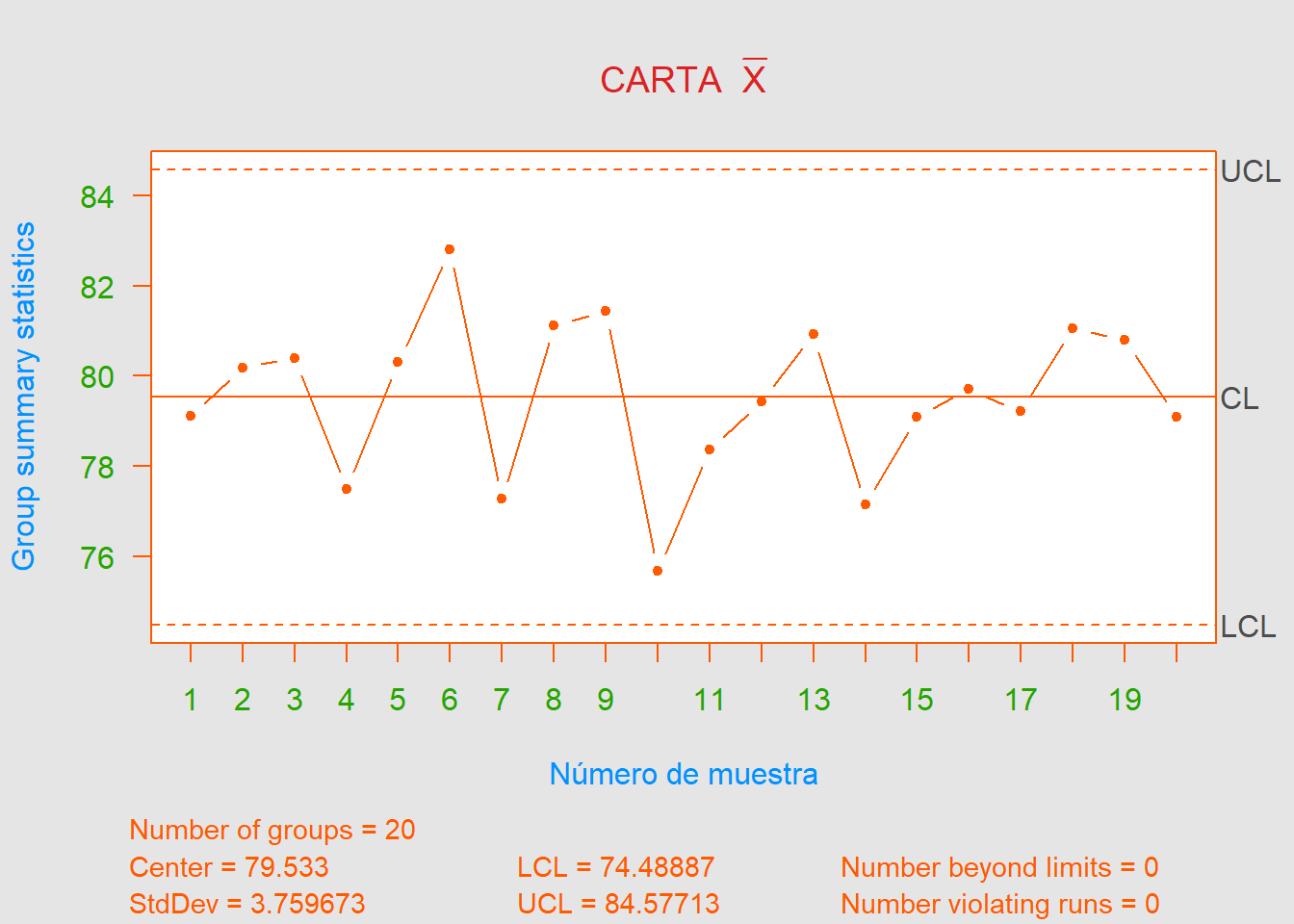
Antes que nada, cabe resaltar que hay un error de digitación en la muestra \(\#9\) (el valor de \(x_4\) no es \(64.1\) sino \(84.1\)). Dicho cambio se realiza ya que para el apartado siguiente (y no podemos eliminar dicho punto ya que no contamos con una causa asignable para él). Sabemos que dicho cambio se debe hacer para que cuadre el valor de \(\overline{x}\) de la muestra \(\#9\), escrito en la tabla.
Finalmente, podemos decir que el proceso está bajo control estadístico.
- b). Después de establecer los cuadros de control en la parte a)., se recogieron \(15\) nuevos subgrupos y las resistencias a la compresión se muestran a continuación. Trace los valores \(\overline{X}\) y \(R\) contra las unidades de control de la parte a). y saque conclusiones.
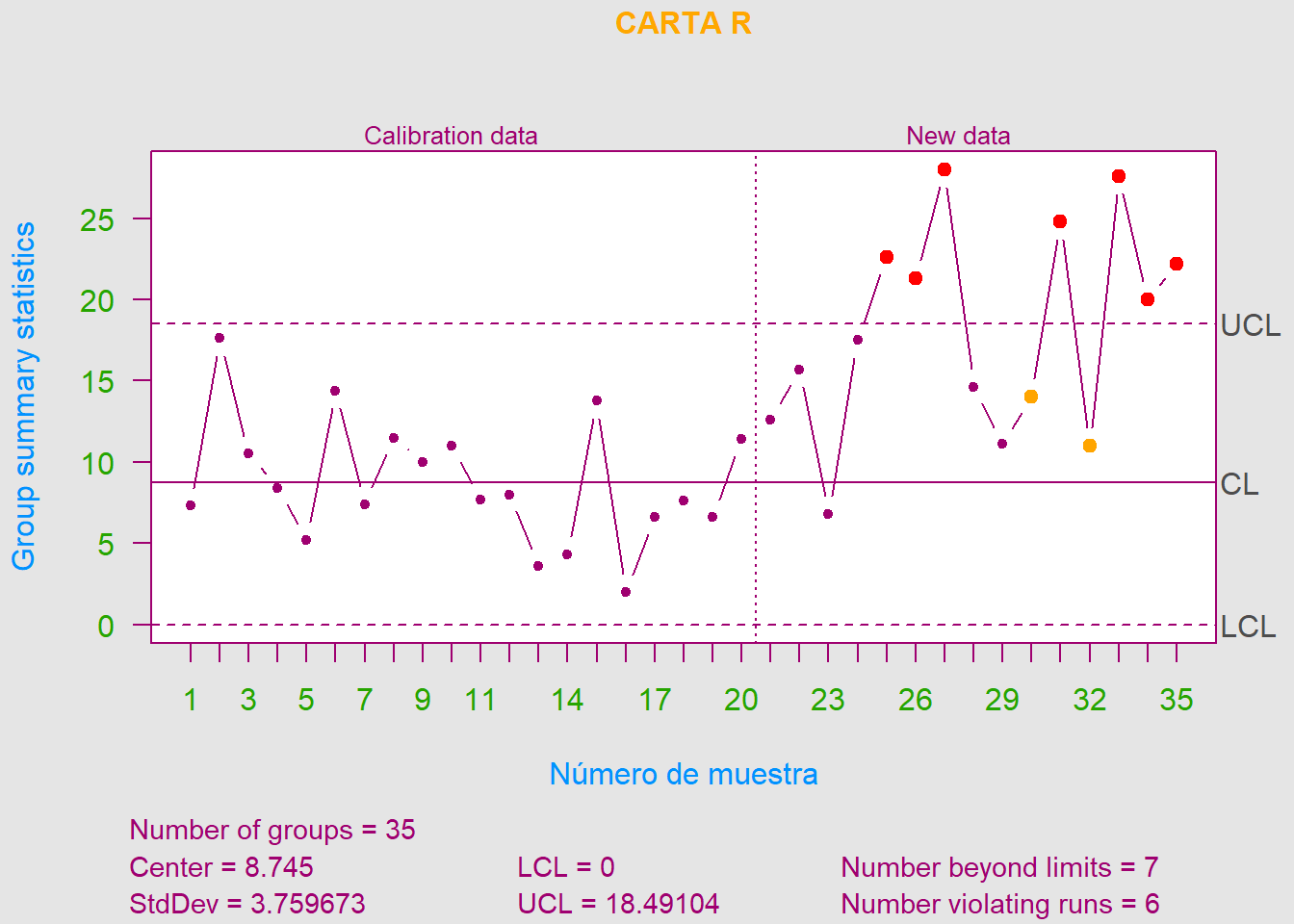
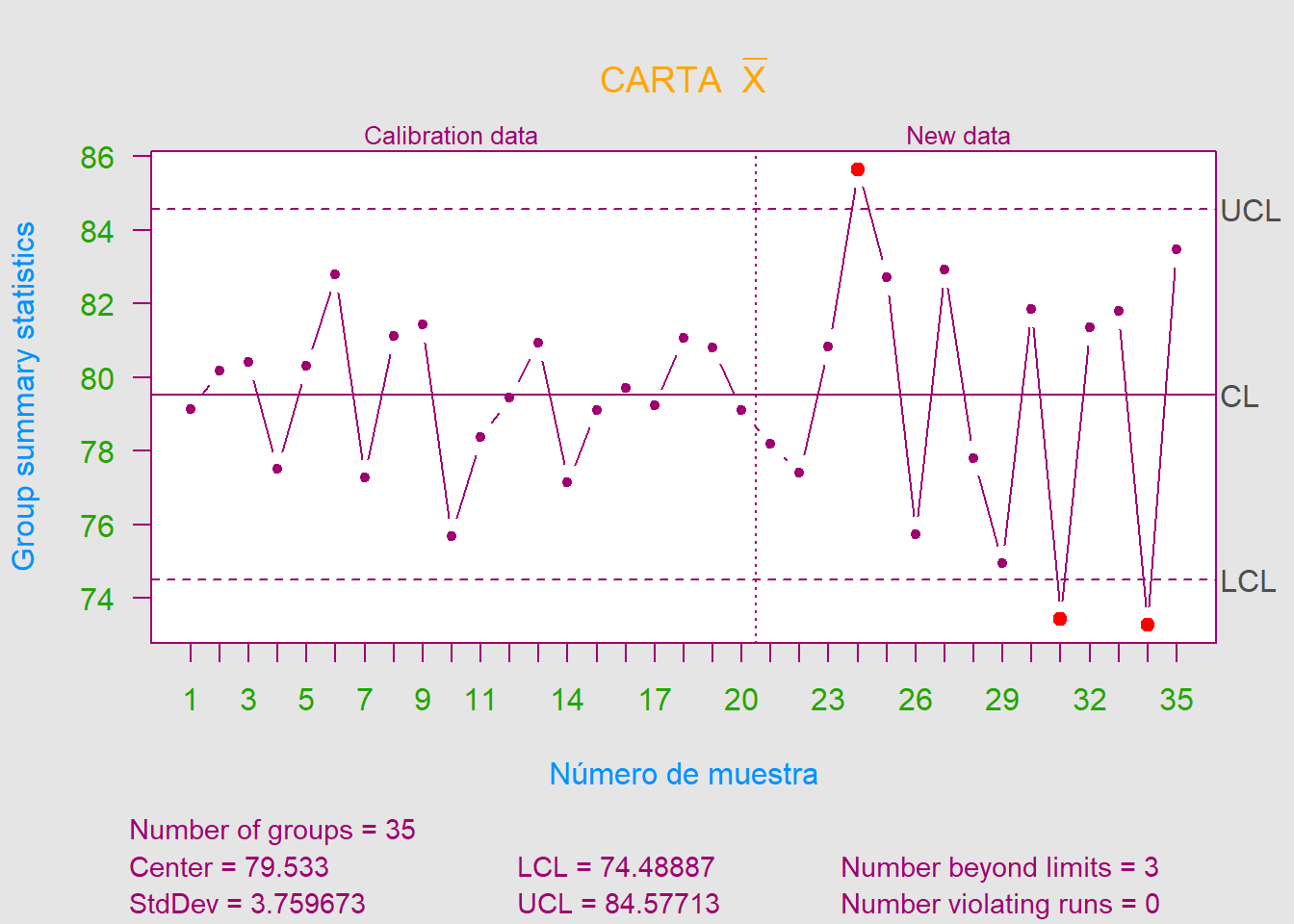
Primero que todo, cabe resaltar que nos encontramos ahora en Fase II (ya que el proceso anterior estaba bajo control). Con esto, podemos observar que varios subgrupos exceden el límite superior de control en la carta \(R\).
5.19
Se utiliza una carta \(\overline{X}\) para controlar la media de una característica de calidad distribuida normal. Se sabe que \(\sigma=6.0\) y \(n=4\). El \(\text{LC}=200\), \(\text{LCS}=209\) y \(\text{LCI}=191\). Si la media del proceso cambia a \(188\), encuentre la probabilidad de que este cambio se detecte en la primera muestra posterior.
\[\begin{align*} \beta &= \textrm{P}(\text{LCI}<\overline{X}<\text{LCS}|\mu_0=188) \\ &= \textrm{P}(\overline{X}<\text{LCS}|\mu_0=188) - \textrm{P}(\overline{X}<\text{LCI}|\mu_0=188) \\ &= \Phi\left( \frac{\text{LCS}-\mu_0}{\sigma/\sqrt{n}} \right)-\Phi\left( \frac{\text{LCI}-\mu_0}{\sigma/\sqrt{n}} \right) \\ &= \Phi\left( \frac{209-188}{6/\sqrt{4}} \right)-\Phi\left( \frac{191-188}{6/\sqrt{4}} \right) \\ &= \Phi(7)-\Phi(1) \\ &= 1-0.8413=0.1587 \end{align*}\]
Donde \(\beta\) es la probabilidad de no detectar dicho cambio. La probabilidad de que se detecte dicho cambio en la primera muestra posterior es \(1-\beta = 1-0.1587 = 0.8413\). Por lo tanto, existe un \(84.13\%\) de posibilidades de que el cambio se detecte en la primera muestra posterior al proceso.
5.26
Las tablas de control en \(\overline{X}\) y \(R\) para muestras de tamaño \(n=5\) deben mantenerse sobre la resistencia a la tracción en libras de un hilo. Para comenzar las cartas, se seleccionaron \(30\) muestras y se calculó la media y el rango de cada uno. Esto produce,
\[\sum_{i=1}^{30} \overline{x}_i = 607.8 \hspace{0.5cm}\text{y}\hspace{0.5cm} \sum_{i=1}^{30} R_i = 144\]
- a). Calcule la línea central y los límites de control para las cartas de control \(\overline{X}\) y \(R\).
\[\begin{align*} \overline{\overline{X}} &= \frac{\sum_{i=1}^{30}\overline{x}_i}{m} = \frac{607.8}{30} = 20.26 \\ \overline{R} &= \frac{\sum_{i=1}^{30}R_i}{m} = \frac{144}{30} = 4.8 \end{align*}\]
Límites para la carta \(\overline{X}\), \[\begin{align*} \text{LCS} &= \overline{\overline{X}}+A_2\overline{R} = 20.26+(0.577\cdot 4.8) = \color{red} {23.03} \\ \text{LC} &= \overline{\overline{X}} = \color{green} {20.26} \\ \text{LCI} &= \overline{\overline{X}}+A_2\overline{R} = 20.26-(0.577\cdot 4.8) = \color{blue} {17.49} \end{align*}\]
Límites para la carta \(R\), \[\begin{align*} \text{LCS} &= \overline{R}D_4 = 4.8\cdot 2.114 = \color{red} {10.15} \\ \text{LC} &= \overline{R} = \color{orange} {4.8} \\ \text{LCI} &= \overline{R}D_3 = 4.8\cdot 0 = \color{blue} {0} \end{align*}\]
- b). Suponga que ambas cartas exhiben control. Hay un límite de especificación inferior único de 16 lb. Si la resistencia se distribuye normal, ¿qué fracción de hilo no cumpliría con las especificaciones?
\[\widehat{\sigma}_x = \frac{\overline{R}}{d_2} = \frac{4.8}{2.326} = \color{purple} {2.064}\] \[\textrm{P}(X<\text{LEI}) = \textrm{P}(X<16) = \textrm{P}\left( Z<\frac{16-20.26}{2.064} \right) = \Phi(-2.064) = \color{magenta} {0.0195}\]
De acuerdo con lo anterior, \(\approx 20\) de cada \(1000\) hilos no cumpliría con las especificaciones (debajo del límite inferior de especificación).
5.48
La viscosidad de un polímero se mide por hora. Las mediciones de las últimas 20 horas se muestran a continuación.
- a). ¿La viscosidad sigue una distribución normal?
Data <- read.delim("../../static/datasets/Exercise 6-63.txt")
soloNumeros <- c(Data$Viscosity)
shapiro.test(soloNumeros) # Prueba de Shapiro-Wilk##
## Shapiro-Wilk normality test
##
## data: soloNumeros
## W = 0.96211, p-value = 0.5869tseries::jarque.bera.test(soloNumeros) # Prueba Jarque-Bera##
## Jarque Bera Test
##
## data: soloNumeros
## X-squared = 1.0734, df = 2, p-value = 0.5847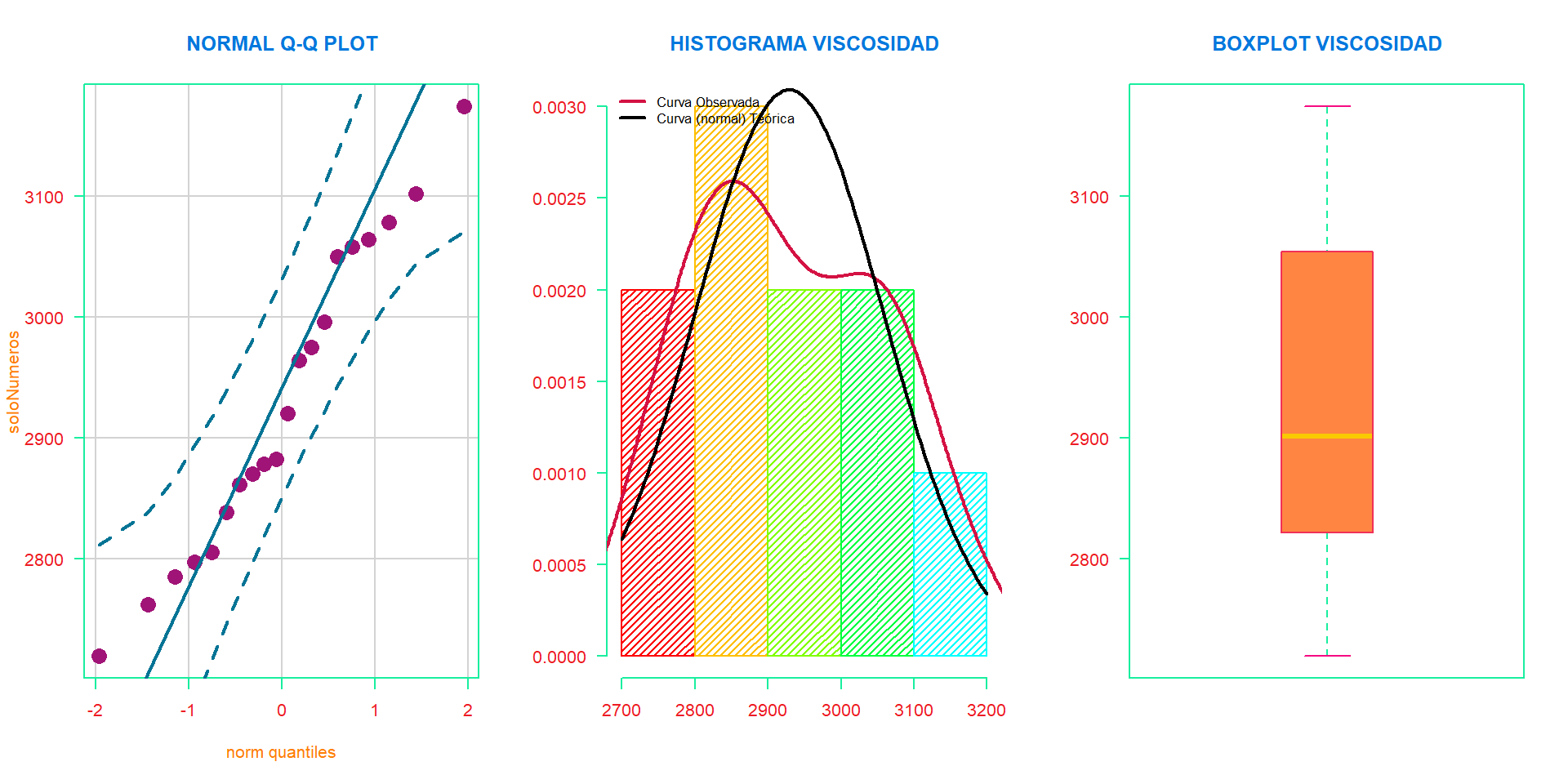
En este caso como el tamaño de muestra no es muy grande (\(n=20\)) no se recomienda usar la prueba de Kolmogorov-Smirnov, usaremos entonces las que se ajusten mejor a nuestro caso. Tanto el test de Shapiro-Wilk como el de Jarque-Bera nos indican que los datos provienen de una distribución normal, ya que el p-valor \(\color{green} {>} \alpha\) por lo tanto no se rechaza \(H_0 :=\) Los datos siguen una distribución normal. Finalmente, podemos afirmar que, con un nivel de confianza del \(95\%\), las mediciones de viscosidad parecen seguir una distribución normal y gráficamente pareciese ser así.
- b). Configure una tabla de control de viscosidad y una tabla de rango móvil. ¿El proceso exhibe control estadístico?
| Viscosidad | Rango Móvil |
|---|---|
| 2838 | NA |
| 2785 | 53 |
| 3058 | 273 |
| 3064 | 6 |
| 2996 | 68 |
| 2882 | 114 |
| 2878 | 4 |
| 2920 | 42 |
| 3050 | 130 |
| 2870 | 180 |
| 3174 | 304 |
| 3102 | 72 |
| 2762 | 340 |
| 2975 | 213 |
| 2719 | 256 |
| 2861 | 142 |
| 2797 | 64 |
| 3078 | 281 |
| 2964 | 114 |
| 2805 | 159 |
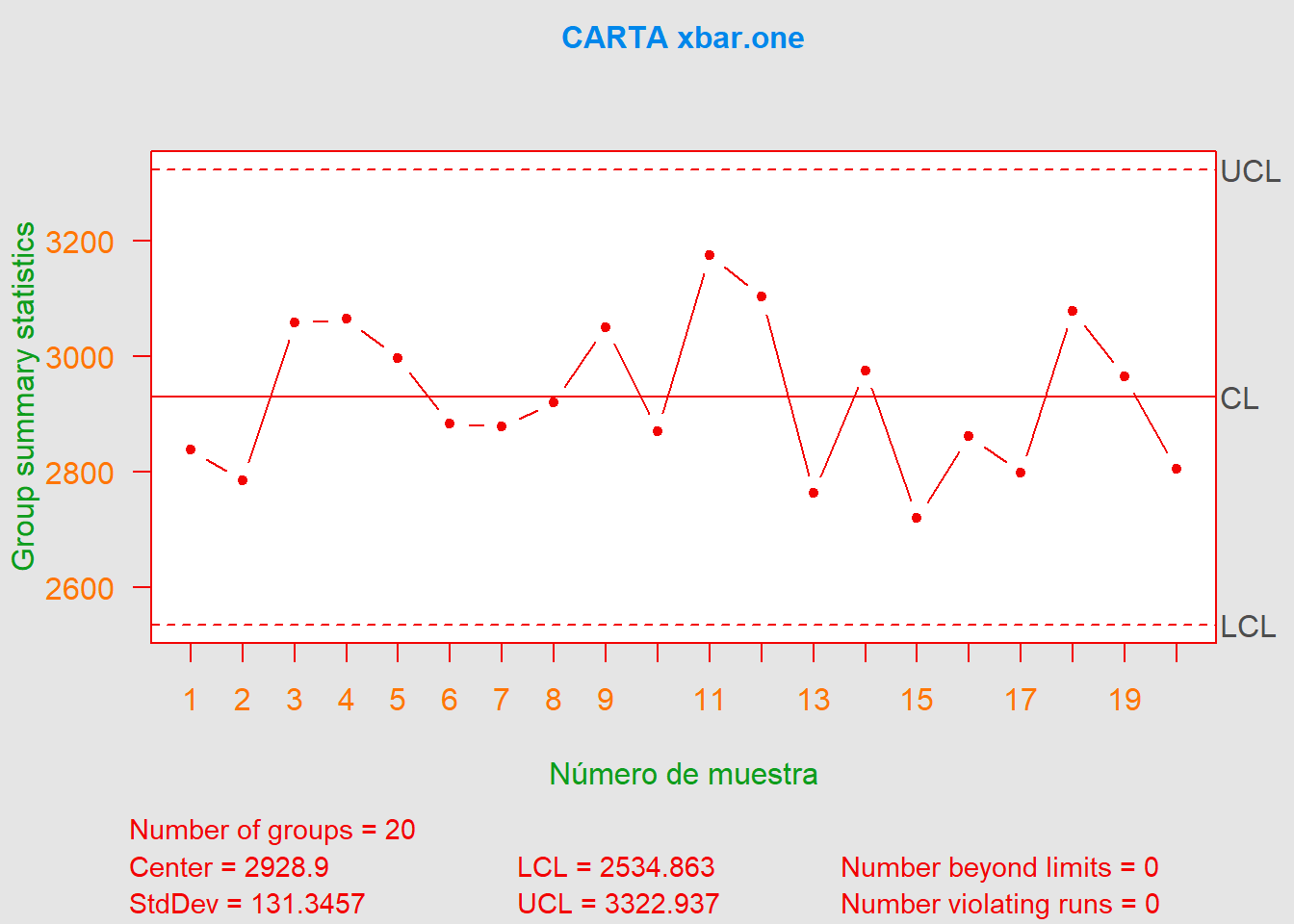
El proceso parece estar bajo control estadístico, ya que no hay observaciones fuera de control en la tabla de control de individuos ni en el gráfico de individuos.
- c). Estime la media y la desviación estándar del proceso.
\[\overline{MR} = \frac{1}{m-1}\sum_{i=1}^{m-1}R_i = \frac{2815}{20-1} = 148.1579\] \[\widehat{\mu} = LC_{\bar{x}} = \color{green} {2928.9} \hspace{0.5cm}\text{y}\hspace{0.5cm} \widehat{\sigma}_x = \frac{\overline{MR}}{d_2} = \frac{148.1579}{1.128} = \color{cyan} {131.3457}\]
Ejercicios Propuestos por el Docente
1). Estimación de punto de cambio
Genere números aleatorios de una \(\mathcal{N}(\mu=0, \sigma^2=1)\) hasta formar 10 subgrupos de tamaño \(n=4\). A partir del subgrupo \(10\) genere las observaciones de una \(\mathcal{N}(\mu_1, 1)\) hasta que la carta \(\overline{X}\) produzca una señal, donde,
\[\mu_1 = \mu_0 + \delta \frac{\sigma}{\sqrt{n}}\]
Calcule el estimador del punto de cambio para, \(\delta = 1.0, 1.5, 2.0, 2.5\) y \(3.0\)
\[\widehat{\tau}_{MLE}= \underset{0\leq t<T}{\text{arg max}}\left \{ (T-t)(\overline{\overline{X}}_{T,t}-\mu_0)^2) \right \}\]
Donde, \[\overline{X}_{T,t}=\frac{1}{T-t}\sum_{i=t+1}^{T}\overline{X}_i\]
A continuación, se expone el código para dicha simulación, tomando como valor de ejemplo \(\delta=1.0\).
set.seed(963852)
NumSample <- 10; TamSample <- 4
mu0 <- 0; sigma <- 1; A <- 3/sqrt(TamSample)
Muestras <- matrix(data = rnorm(NumSample*TamSample, mu0, sigma),
nrow = NumSample, ncol = TamSample)
delta <- 3.0 # Luego con 1.25,2.0,2.5 y 3.0
mu1 <- mu0 + delta*(sigma/sqrt(TamSample))
CartaXbar <- qcc(Muestras, type = "xbar", center = mu0,
limits = c(mu0-A*sigma,mu0+A*sigma), plot = FALSE)
Prueba <- sum(CartaXbar$violations$beyond.limits)
while (Prueba==0) {
x <- rnorm(n = TamSample, mean = mu1, sd = 1)
Muestras <- rbind(Muestras, x)
rownames(Muestras) <- 1:nrow(Muestras)
CartaXbar <- qcc(Muestras, type = "xbar", center = mu0,
limits = c(mu0-A*sigma,mu0+A*sigma), plot = FALSE)
Prueba <- sum(CartaXbar$violations$beyond.limits)
}
New_CartaXbar <- qcc(Muestras, type = "xbar", center = mu0,
limits = c(mu0-A*sigma,mu0+A*sigma), plot = FALSE)
T <- New_CartaXbar$violations$beyond.limits
Estimador <- NULL
for (i in 0:(T-1)) {
if (i==T-1) { xbarbar <- mean(Muestras[1:(T-i), ]) }
else { xbarbar <- mean(rowMeans(Muestras[1:(T-i), ])) }
Estimador[i] <- (T-i)*((xbarbar-mu0)^2)
}
Estimador_tau <- c(1:(T-1))[Estimador==max(Estimador)]
c("Delta" = delta, "Estimador_tau" = Estimador_tau)Finalmente, para todos los valores de \(\delta\) obtenemos el estimador del punto de cambio para la media \(\widehat{\tau}_{MLE}\), obteniendo como resultado,
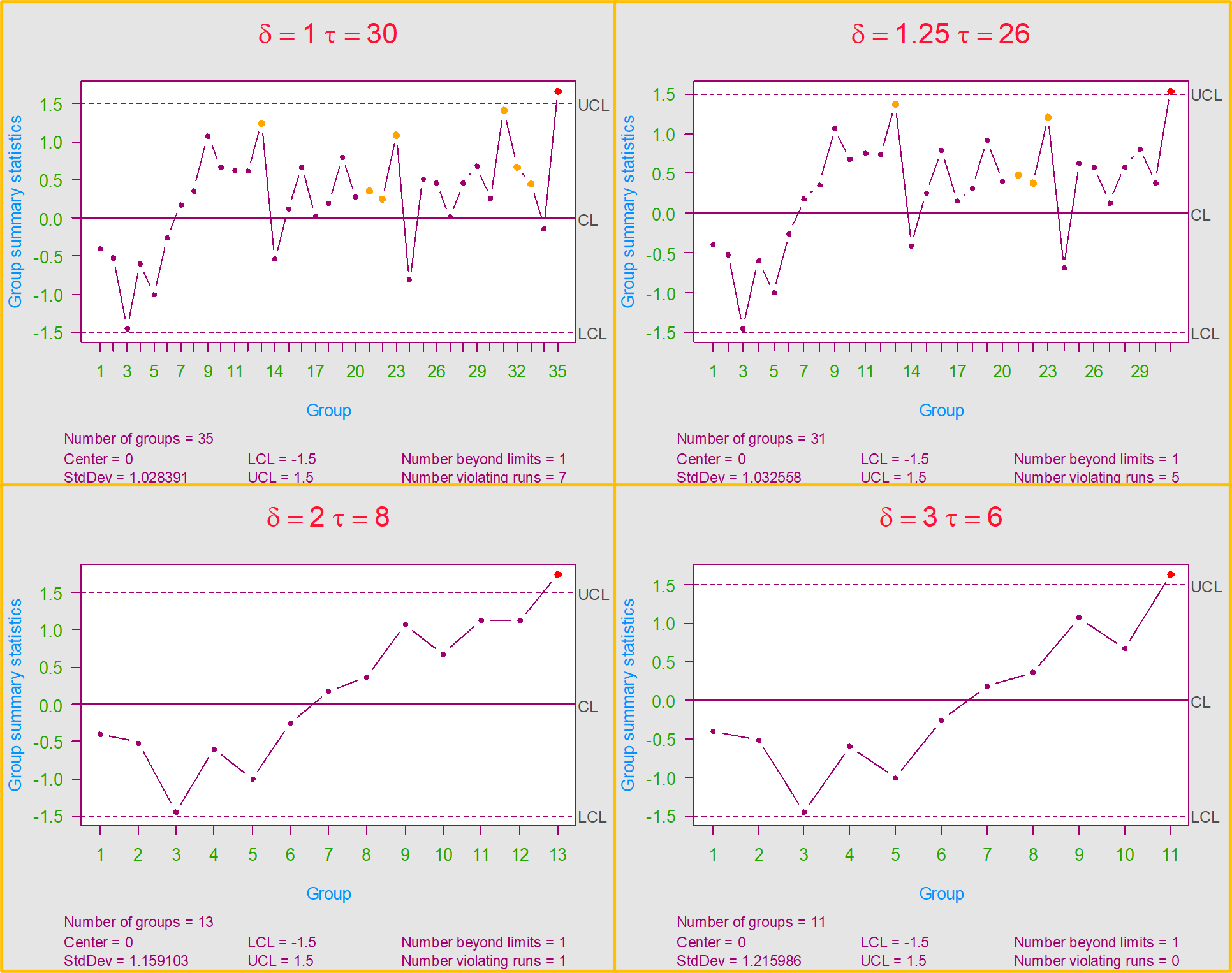
| \(\delta\) | 1.0 | 1.25 | 2.0 | 2.5 | 3.0 |
|---|---|---|---|---|---|
| \(\widehat{\tau}_{MLE}\) | 30 | 26 | 8 | 8 | 6 |
Podemos observar que para \(\delta=1.0\) se necesitaron 35 subgrupos más para que la carta \(\overline{X}\) diera una señal, mientras que para \(\delta=3.0\) solo se necesita un subgrupo más para que la carta diera una señal. El estimador del punto de cambio para el primer caso fue 30, es decir, que en el subgrupo 30 se dio un cambio en la media. Finalmente, para \(\delta\geq 3.0\) el estimador del punto de cambio tiende a mantenerse constante indicando que fue en el subgrupo 6 donde se dio dicho cambio.
Cabe resaltar que los límites de control, en la simulación, no deben cambiar porque conocemos los parámetros poblacionales.
2). Capacidad de procesos
Genere \(100\) números aleatorios de una \(\mathcal{N}(\mu=10, \sigma^2=9)\). Asuma que \(\text{LEI} = 2\) y \(\text{LES} = 18\). Estime \(\mu\) y \(\sigma\) y calcule \(\widehat{C}_p\), \(\widehat{C}_{pk}\) y \(\widehat{C}_{pm}\). Construya un \(\text{I.C}_{(1-\alpha)\%}\) para \(C_p\).
\[\begin{align*} \widehat{C}_{p} &= \frac{LES-LEI}{6\widehat{\sigma}} \\ \widehat{C}_{pk} &= \widehat{C}_{p} \left\{ 1-\frac{|\overline{X}-M|}{d} \right\} \\ \widehat{C}_{pm} &= \frac{LES-LEI}{6\sqrt{\frac{\sum_{i=1}^{n} (X_i-T)^2}{n-1}}} \end{align*}\]
Donde \(d=(LES-LEI)/2\) y \(M=(LES+LEI)/2\).
set.seed(666666)
LEI <- 2; LES <- 18; n <- 100
# Cuando se dan los límites de especificación se asume que el valor objetivo T es el promedio.
T <- (LEI+LES)/2
Xi <- rnorm(n, mean = 10, sd = 3)
xBarra <- mean(Xi); SigmaEst <- sd(Xi)
C_p <- (LES-LEI)/(6*SigmaEst)
d <- (LES-LEI)/2; M <- (LES+LEI)/2
C_pk <- C_p*(1-(abs(xBarra-M)/d))
C_pm <- (LES-LEI)/(6*sqrt( sum((Xi-T)^2)/(n-1) ))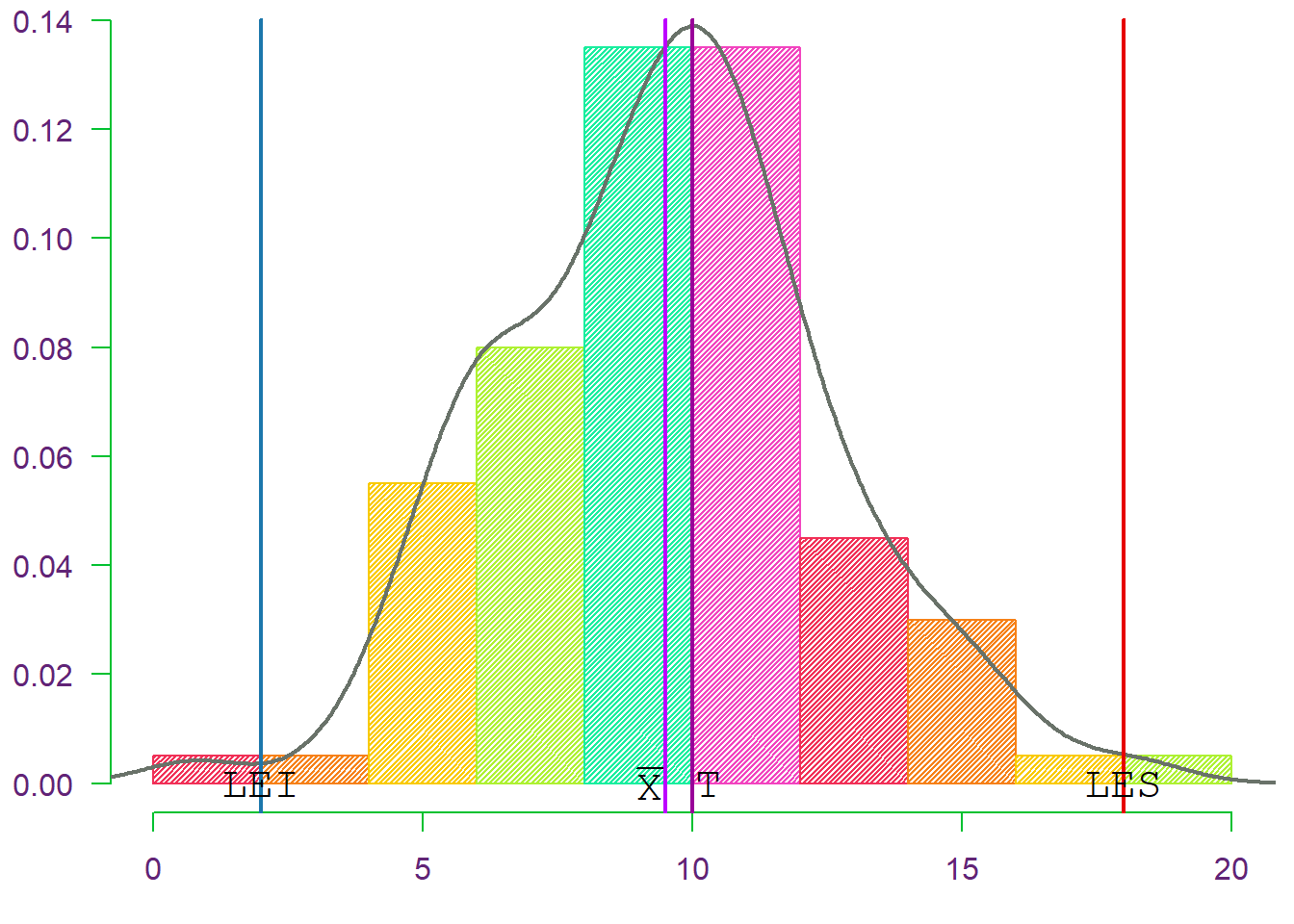
| Proceso | mu | sigma | Cp | Cpk | Cpm |
|---|---|---|---|---|---|
| A | 9.4962 | 3.0306 | 0.8799 | 0.8245 | 0.8679 |
El proceso anterior revela que la media del proceso está centrada aproximadamente en el punto medio del intervalo de especificaciones con una desviación estándar muestral de \(3.03\). Los 3 índices no coinciden, siendo el mayor el \(\widehat{C}_p\), aunque este no tiene en cuenta desvíos de \(\mu\) respecto de \(T\). Por último, observamos que ninguno de ellos es \(\geq 1\), que es lo que se busca en un proceso productivo.
\[\text{I.C}_{(1-\alpha)\%}(C_p)=\left ( \widehat{C}_p \sqrt{\frac{\chi^{2}_{(n-1,\frac{\alpha}{2})}}{n-1}}, \,\, \widehat{C}_p \sqrt{\frac{\chi^{2}_{(n-1,1-\frac{\alpha}{2})}}{n-1}} \right )\]
Alpha <- 0.95
LimInf <- C_p*sqrt( qchisq(p = Alpha/2, df = n-1)/(n-1) )
LimSup <- C_p*sqrt( qchisq(p = 1-(Alpha/2), df = n-1)/(n-1) )
c("Lim_Inf" = LimInf, "Lim_Sup" = LimSup)## Lim_Inf Lim_Sup
## 0.8730433 0.8808814Finalmente, un intervalo de confianza del \(95\%\) de confianza para \(C_p\) es, \[\text{I.C}_{95\%}(C_p) = (\color{cyan} {0.873}, \,\,\color{red} {0.881})\]
SOLUCIÓN TALLER #2
Exercises Introduction to Statistical Quality Control Montgomery
6.1
Los siguientes datos dan el número de conjuntos de rodamientos y sellos no conformes en muestras de tamaño \(100\). Construya una carta de control de fracción no conforme para estos datos. Si alguno de los puntos está fuera de control, suponga que se pueden encontrar causas asignables y determine los límites de control revisados.
\[\begin{align*} LCS &= \overline{p}+3\sqrt{\frac{\overline{p}(1-\overline{p})}{n}} = 0.0585+3\sqrt{\frac{0.0585(1-0.0585)}{100}} = \color{red} {0.1289} \\ LC &= \overline{p} = \color{orange} {0.0585} \\ LCI &= \overline{p}+3\sqrt{\frac{\overline{p}(1-\overline{p})}{n}} = 0.0585-3\sqrt{\frac{0.0585(1-0.0585)}{100}} = \color{cyan} {0} \end{align*}\]
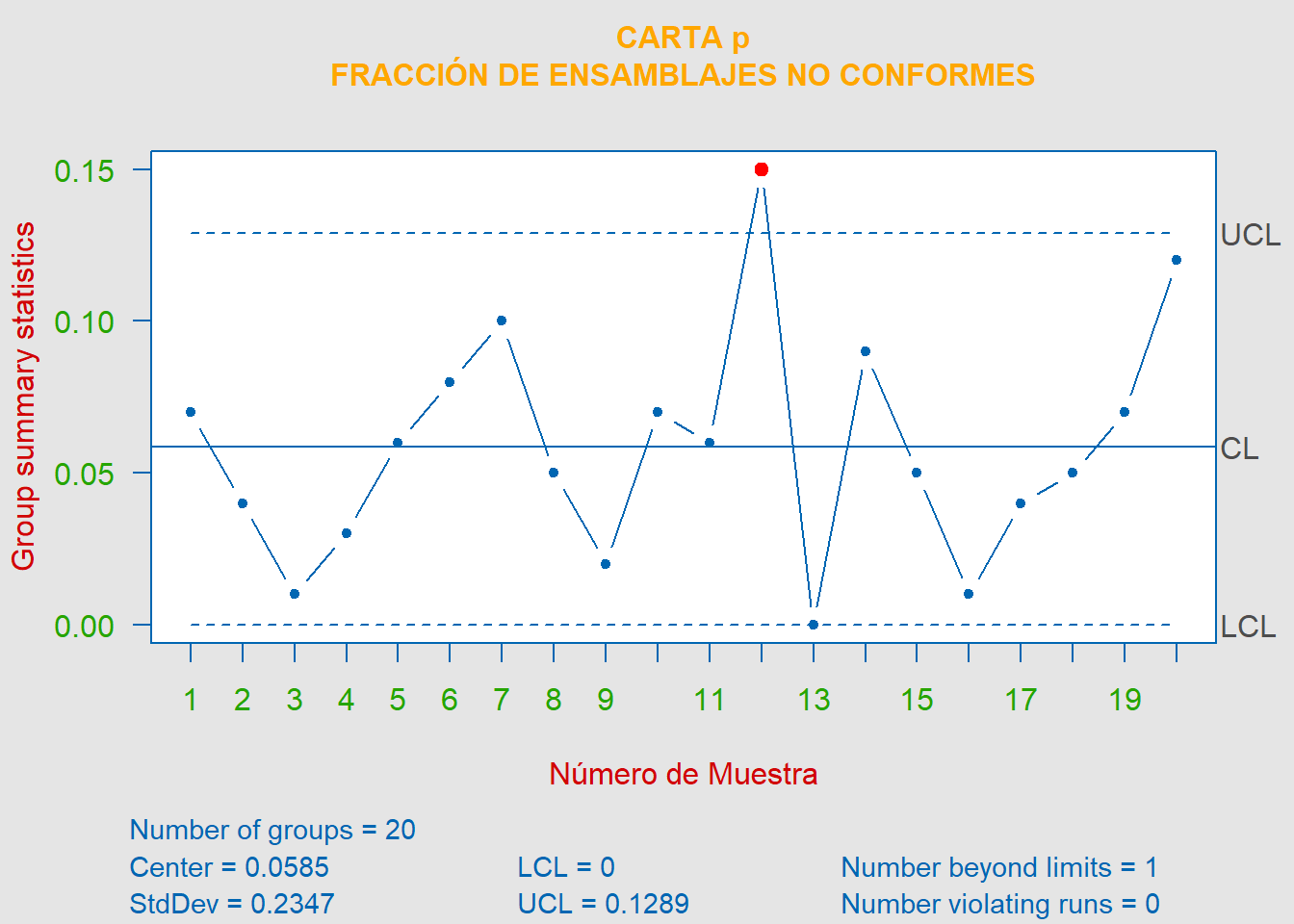
La carta de control para la fracción no conforme de rodamientos y sellos, la cual no se encuentra bajo control estadístico, queda definida por los límites, \(LCS = 0.1289 \hspace{0.25cm}|\hspace{0.25cm} \overline{P} = 0.0585 \hspace{0.25cm}|\hspace{0.25cm} LCI = 0\).
Ahora eliminando la muestra \(\#12\), ya que suponemos que se encontró una causa asignable para éste, tenemos que,
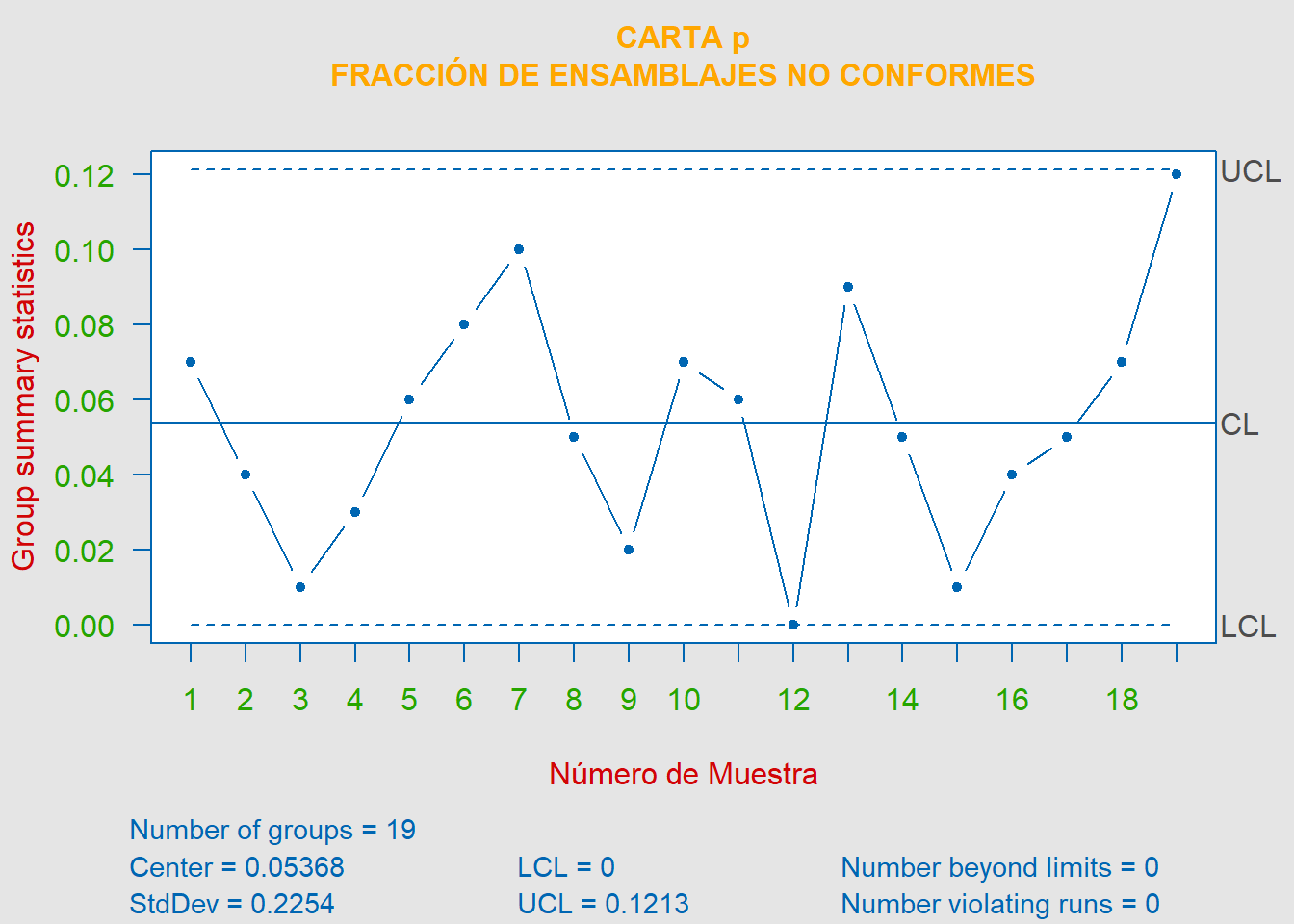
\[\begin{align*} LCS &= \overline{p}+3\sqrt{\frac{\overline{p}(1-\overline{p})}{n}} = 0.0537+3\sqrt{\frac{0.0537(1-0.0537)}{100}} = \color{red} {0.1213} \\ LC &= \overline{p} = \color{green} {0.0537} \\ LCI &= \overline{p}+3\sqrt{\frac{\overline{p}(1-\overline{p})}{n}} = 0.0537-3\sqrt{\frac{0.0537(1-0.0537)}{100}} = \color{cyan} {0} \end{align*}\]
Finalmente, eliminando la muestra número 12, ya que suponemos que se encontraron causas asignables para dicha muestra, la nueva carta, la cual se encuentra ahora bajo control estadístico, queda definida mediante, \(LCS = 0.1213 \hspace{0.25cm}|\hspace{0.25cm} \overline{P} = 0.0537 \hspace{0.25cm}|\hspace{0.25cm} LCI = 0\).
6.4
Un proceso que produce piezas forjadas de titanio para las ruedas de turbocompresor de automóviles se controlará mediante el uso de una carta de fracción no conforme. Inicialmente, se toma una muestra de tamaño \(150\) cada día durante 20 días, y se observan los resultados que se muestran aquí.
- a). Establezca una carta de control para monitorear la producción futura.
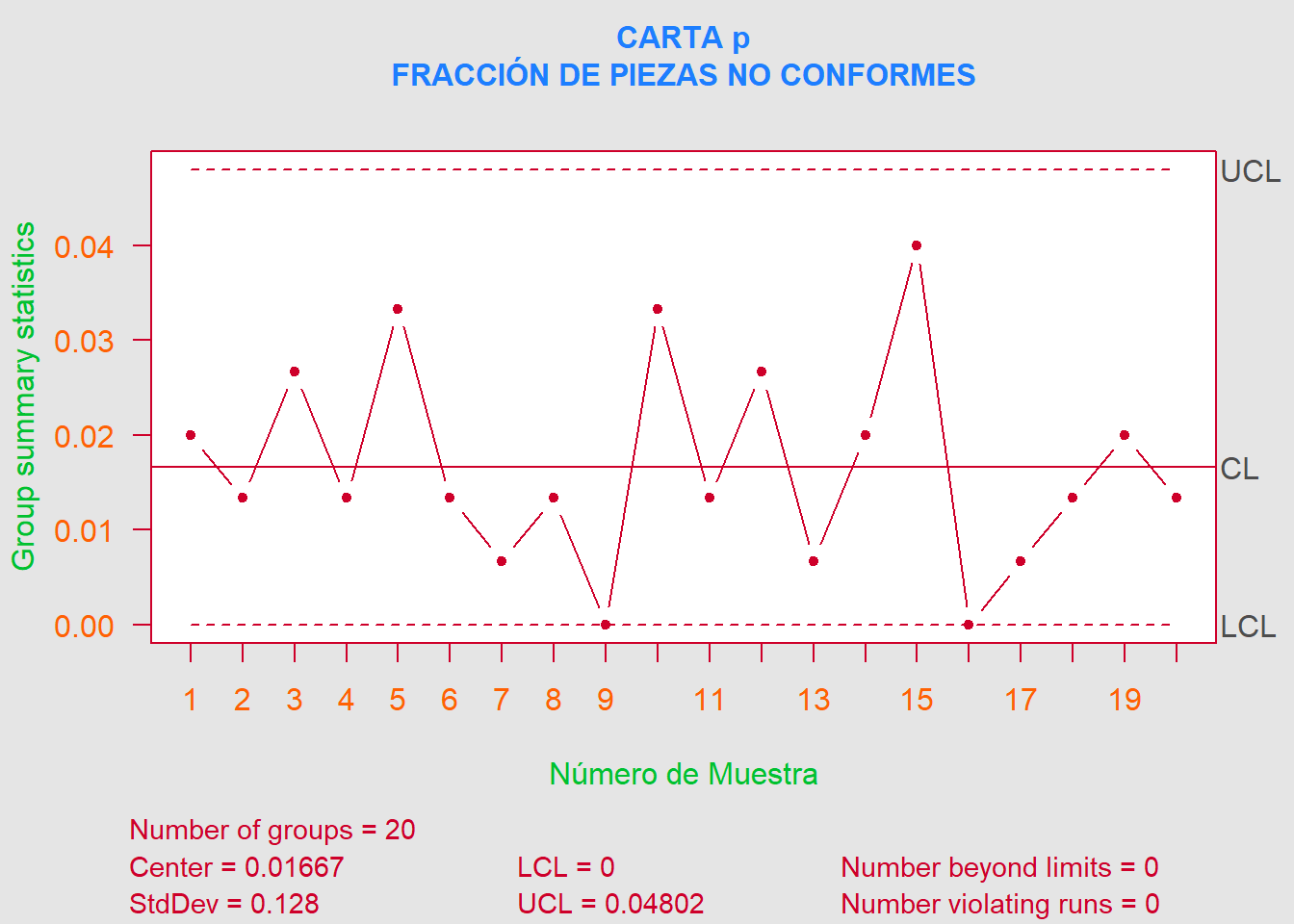
- b). ¿Cuál es el tamaño de muestra más pequeño que podría usarse para este proceso y aún así dar un límite de control inferior positivo en la carta?
Asumiendo que \(L=3\) sigma, como es lo usual, el tamaño de muestra mínimo para lograr un límite de control inferior positivo es,
\[\begin{align*} LCI &= \overline{p}-L\sqrt{\frac{\overline{p}(1-\overline{p})}{n}}\geq 0 \\ \color{green} {\therefore}\,\, n &> \frac{1-\overline{p}}{\overline{p}}\cdot L^2 \\ &> \frac{1-0.0167}{0.0167}\cdot 3^2 \\ &> \color{magenta} {529.922} \approx \color{purple} {530} \end{align*}\]
Por lo tanto, \(n = 530\) es el tamaño de muestra más pequeño para que la carta de control tenga un \(LCI\) positivo.
6.6
Según los siguientes datos, si se va a establecer una carta \(np\), ¿cuál recomendaría como la línea central y los límites de control? Suponga que \(n = 500\).
\[\begin{align*} LCS &= n\overline{p}+3\sqrt{n\overline{p}(1-\overline{p})} = 4+3\sqrt{4\cdot (1-0.008)} = \color{red} {9.976} \\ LC &= n\overline{p} = 500\cdot 0.008 = \color{orange} {4} \\ LCI &= n\overline{p}-3\sqrt{n\overline{p}(1-\overline{p})} = 4-3\sqrt{4\cdot (1-0.008)} = \color{cyan} {0} \end{align*}\]
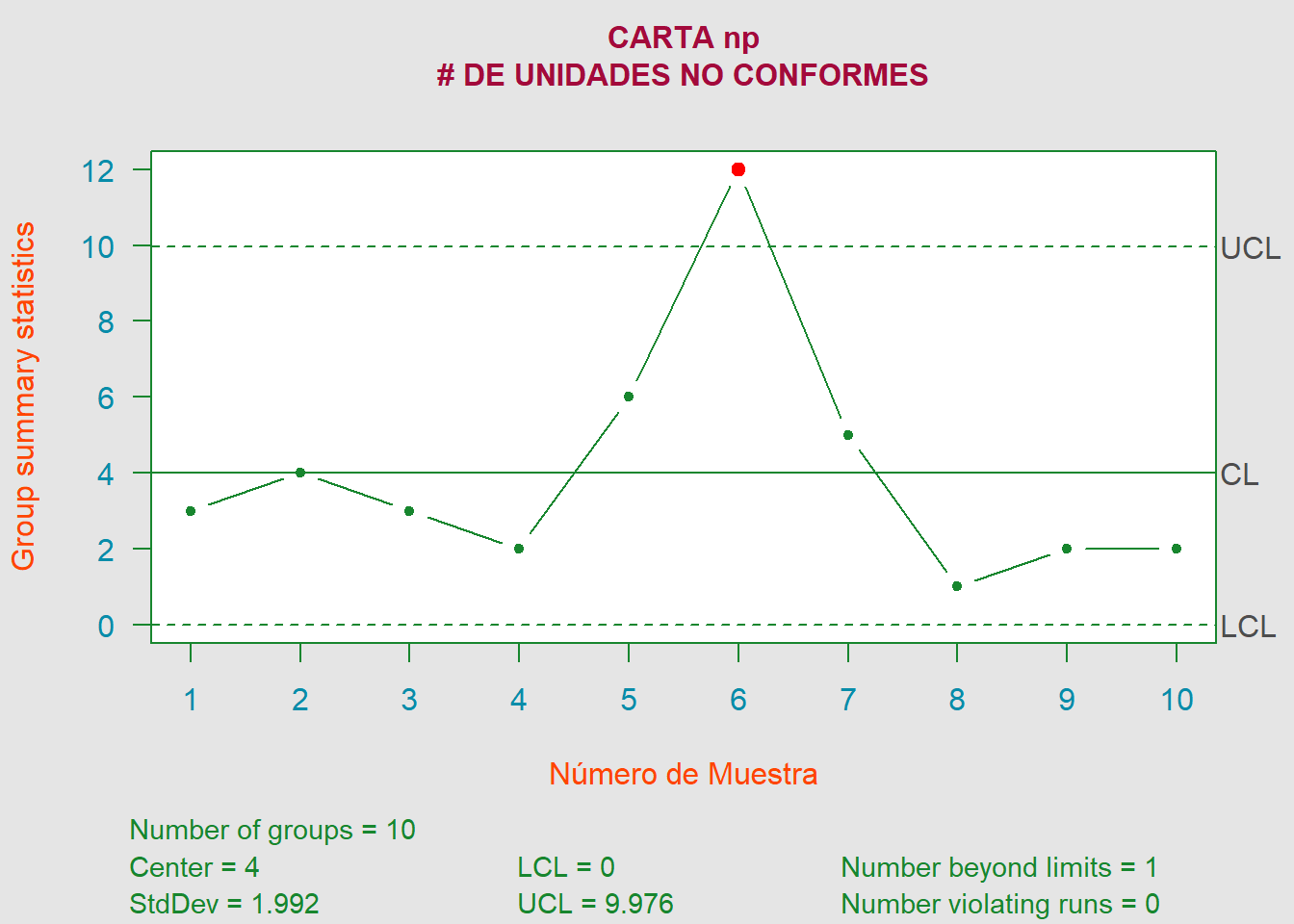
Recalculando los límites de control sin la muestra \(\#6\), ya que suponemos que se encontraron causas asignables para dicha muestra, la nueva carta, la cual se encuentra ahora bajo control estadístico, queda definida mediante, \(LCS = 8.39 \hspace{0.25cm}|\hspace{0.25cm} n\overline{p} = 3.11 \hspace{0.25cm}|\hspace{0.25cm} LCI = 0\), los cuales son la línea central y los límites de control recomendados.
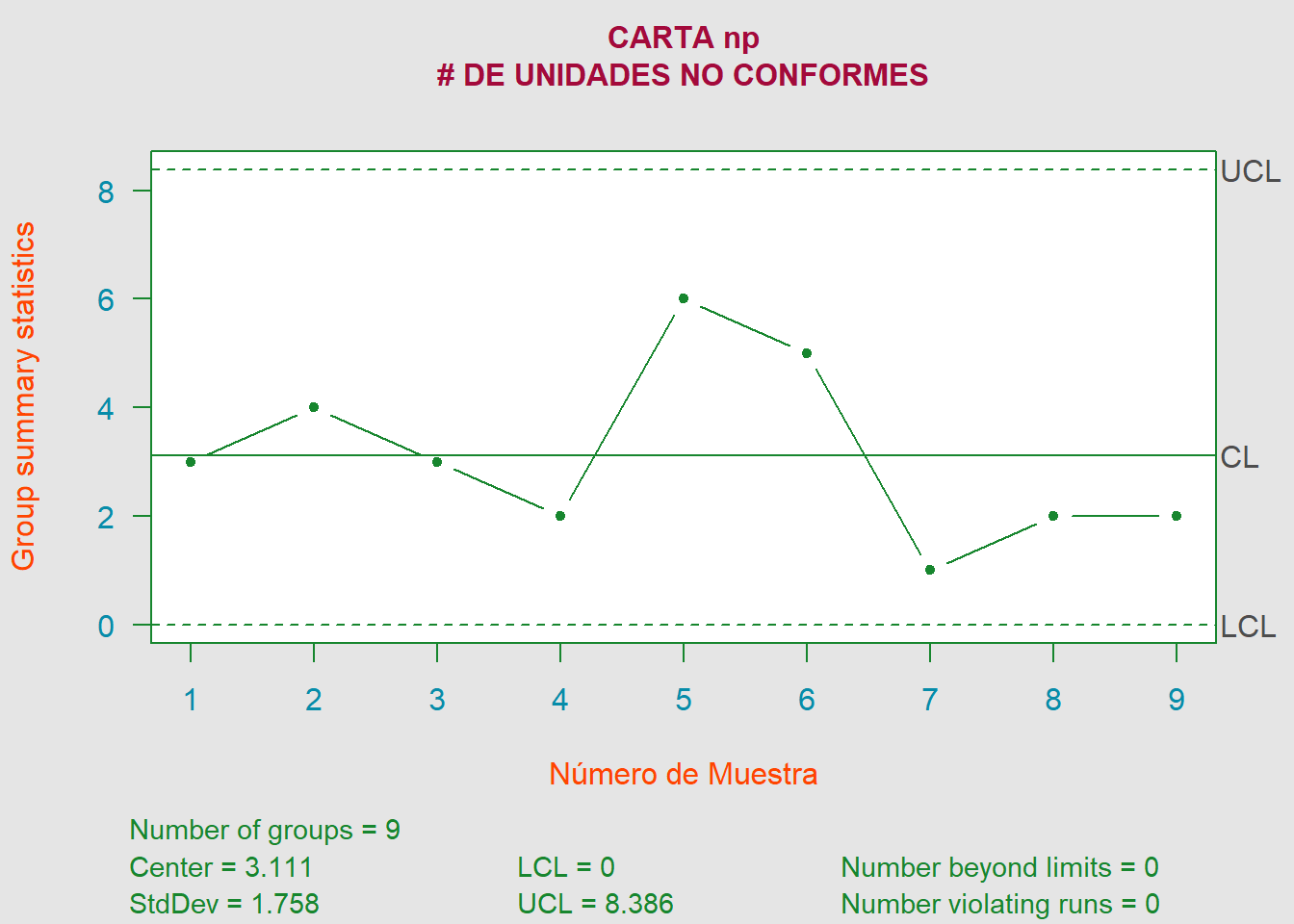
6.36
Los defectos superficiales se han contado en \(25\) placas de acero rectangulares, y los datos se muestran aquí. Configure una carta de control para las no conformidades utilizando estos datos. ¿El proceso que produce las placas parece estar bajo control estadístico?
| No. Plato | No. de Inconformidades | No. Plato | No. de Inconformidades |
|---|---|---|---|
| 1 | 1 | 14 | 0 |
| 2 | 0 | 15 | 2 |
| 3 | 4 | 16 | 1 |
| 4 | 3 | 17 | 3 |
| 5 | 1 | 18 | 5 |
| 6 | 2 | 19 | 4 |
| 7 | 5 | 20 | 6 |
| 8 | 0 | 21 | 3 |
| 9 | 2 | 22 | 1 |
| 10 | 1 | 23 | 0 |
| 11 | 1 | 24 | 2 |
| 12 | 0 | 25 | 4 |
| 13 | 8 |
\[\begin{align*} LCS &= \overline{c}+3\sqrt{\overline{c}} = 2.36+3\sqrt{2.36} = \color{red} {6.9687} \\ LC &= \overline{c} = \color{green} {2.36} \\ LCI &= \overline{c}-3\sqrt{\overline{c}} = 2.36-3\sqrt{2.36} = \color{cyan} {0} \end{align*}\]
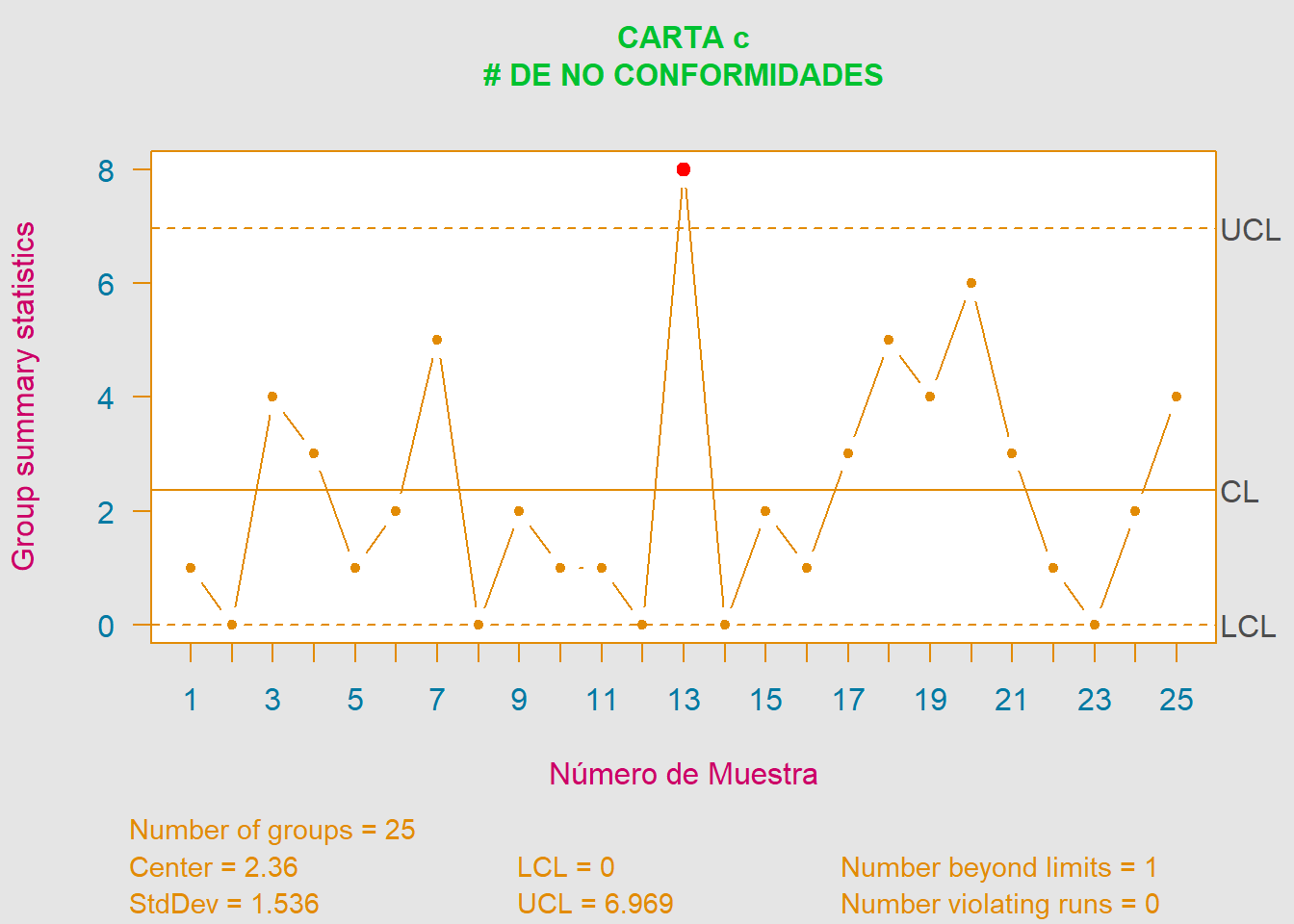
De acuerdo con la carta de control c podemos observar que el proceso de placas de acero rectangulares no parece estar bajo control estadístico, pues la muestra \(\#13\) supera el \(LCS\). Por lo que se debería detener el proceso y buscar alguna causa asignable a dicho dato.
6.37
Una fábrica de papel utiliza un cuadro de control para controlar la imperfección en los rollos de papel terminados. La producción se inspecciona durante \(20\) días y los datos resultantes se muestran aquí. Use estos datos para configurar una carta de control de no conformidades por rollo de papel. ¿El proceso parece estar en control estadístico? ¿Qué línea central y límites de control recomendaría para controlar la producción actual?
| Día | No. de Rollos | Imperfecciones | Día | No. de Rollos | Imperfecciones |
|---|---|---|---|---|---|
| 1 | 18 | 12 | 11 | 18 | 18 |
| 2 | 18 | 14 | 12 | 18 | 14 |
| 3 | 24 | 20 | 13 | 18 | 9 |
| 4 | 22 | 18 | 14 | 20 | 10 |
| 5 | 22 | 15 | 15 | 20 | 14 |
| 6 | 22 | 12 | 16 | 20 | 13 |
| 7 | 20 | 11 | 17 | 24 | 16 |
| 8 | 20 | 15 | 18 | 24 | 18 |
| 9 | 20 | 12 | 19 | 22 | 20 |
| 10 | 20 | 10 | 20 | 21 | 27 |
\[\begin{align*} LCS &= \overline{u}+3\sqrt{\overline{u}/n_i} = \color{red} {0.7007+3\sqrt{0.7007/n_i}} \\ LC &= \overline{u} = \color{orange} {0.7007} \\ LCI &= \overline{u}-3\sqrt{\overline{u}/n_i} = \color{cyan} {0.7007-3\sqrt{0.7007/n_i}} \end{align*}\]
No.Imperfecciones <- c(12,14,20,18,15,12,11,15,12,10,18,14,9,10,14,13,16,18,20,17)
No.RollosProducidos <- c(18,18,24,22,22,22,20,20,20,20,18,18,18,20,20,20,24,24,22,21)
Data <- cbind(No.Imperfecciones, No.RollosProducidos) %>% as.data.frame()
Ubarra <- sum(Data$No.Imperfecciones)/sum(Data$No.RollosProducidos)
ni <- sort(unique(Data$No.RollosProducidos))
LimInf <- Ubarra-(3*sqrt(Ubarra/ni)); LimSup <- Ubarra+(3*sqrt(Ubarra/ni))
Tabla <- data.frame("n_i" = ni, "LCI_i" = LimInf, "LCS_i" = LimSup)
# ---------------------------------- TABLA HTML ---------------------------------- #
kable(Tabla, "html", booktabs = T, align = "c", digits = 4) %>%
kable_styling(bootstrap_options = Form.Basic, full_width = F)| n_i | LCI_i | LCS_i |
|---|---|---|
| 18 | 0.1088 | 1.2926 |
| 20 | 0.1392 | 1.2623 |
| 21 | 0.1527 | 1.2487 |
| 22 | 0.1653 | 1.2361 |
| 24 | 0.1881 | 1.2133 |
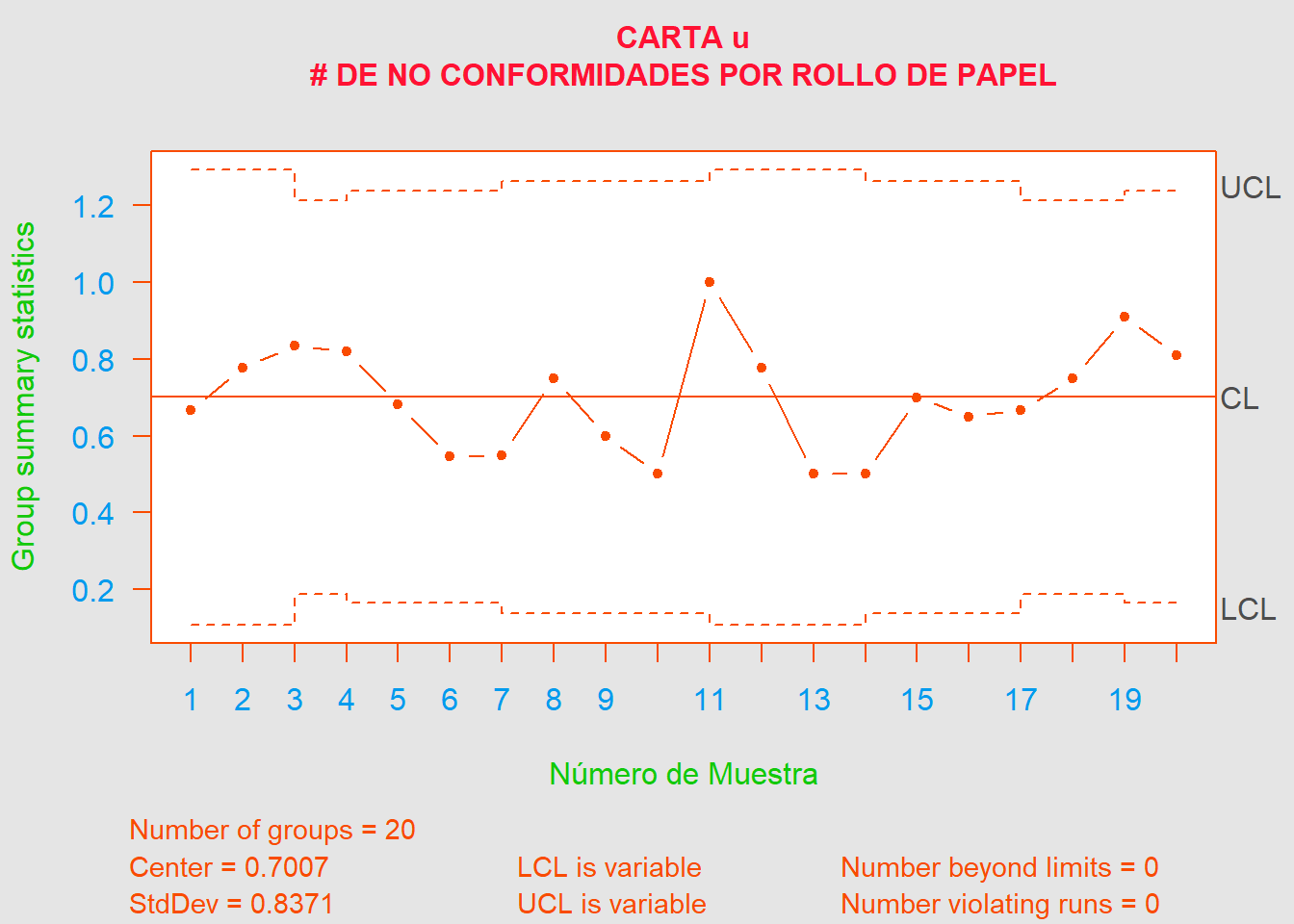
De acuerdo con la carta de control u el proceso parece estar bajo control estadístico. Recomendaría tomar, tanto el \(LCI\) como el \(LCS\), usados cuando \(n=21\) (para así obtener limites constantes), dado que es el valor promedio de los \(n\) (\(\overline{n} = 20.55 \approx 21\)) y representa mejor la distribución de los datos. Por lo tanto, la carta queda definida mediante, \(LCS = 1.249 \hspace{0.25cm}|\hspace{0.25cm} LC = 0.701 \hspace{0.25cm}|\hspace{0.25cm} LCI = 0.153\).
8.1
Los siguientes datos representan observaciones individuales sobre el peso molecular tomado por hora de un proceso químico. El valor objetivo del peso molecular es \(1050\) y se cree que la desviación estándar del proceso es aproximadamente \(\sigma = 25\).
| No. Observación | \(x\) | No. Observación | \(x\) |
|---|---|---|---|
| 1 | 1045 | 11 | 1139 |
| 2 | 1055 | 12 | 1169 |
| 3 | 1037 | 13 | 1151 |
| 4 | 1064 | 14 | 1128 |
| 5 | 1095 | 15 | 1238 |
| 6 | 1008 | 16 | 1125 |
| 7 | 1050 | 17 | 1163 |
| 8 | 1087 | 18 | 1188 |
| 9 | 1125 | 19 | 1146 |
| 10 | 1146 | 20 | 1167 |
- a). Configure un CUSUM tabular para la media de este proceso. Diseñe la carta CUSUM para detectar rápidamente un cambio de aproximadamente \(1.0\sigma\) en la media del proceso.
\[\begin{align*} K &= \frac{\delta}{2}\cdot \sigma = \frac{1}{2}\cdot (25) = \color{purple} {12.5} \\ H &= 5\cdot \sigma = 5\cdot 25 = \color{magenta} {125} \end{align*}\]
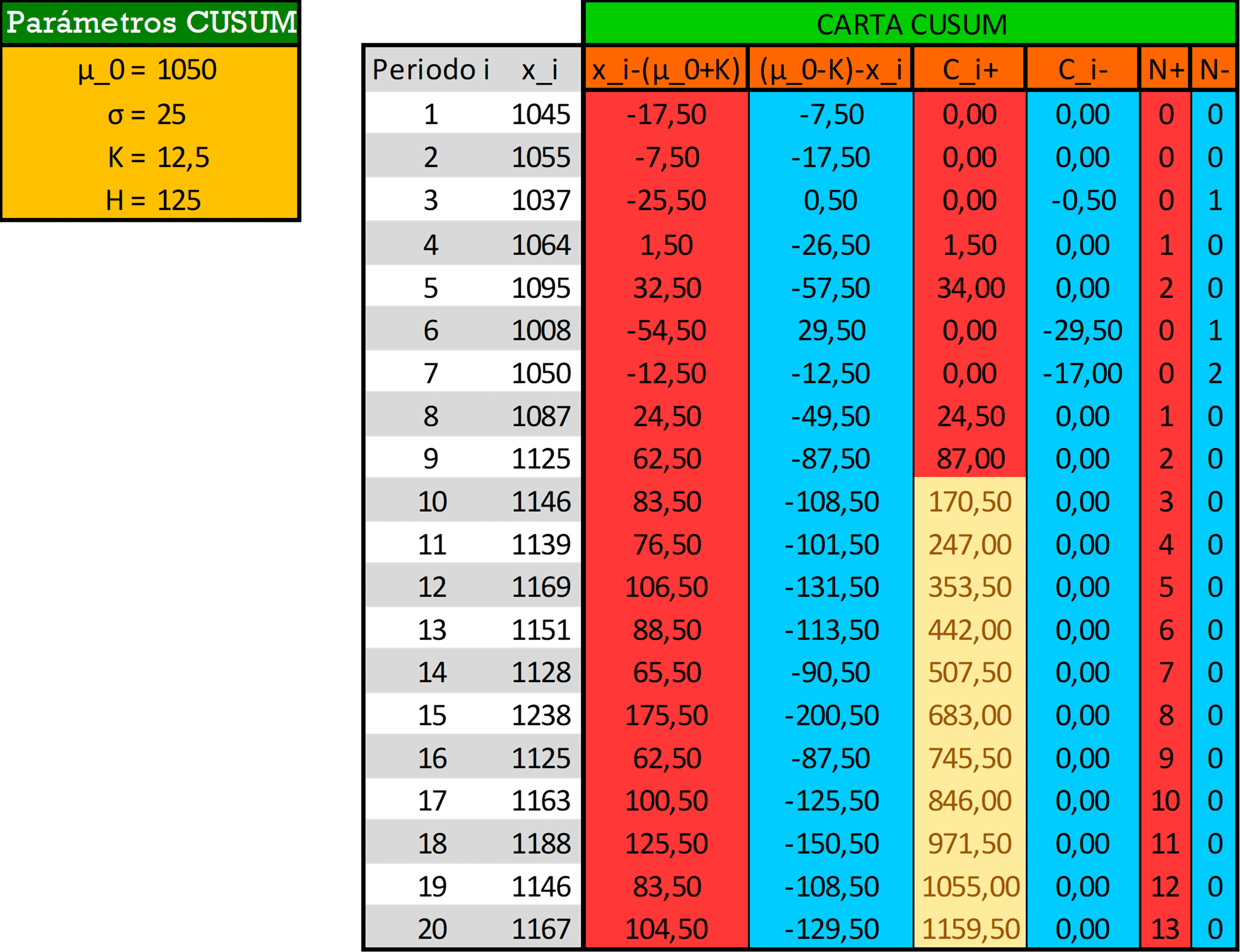
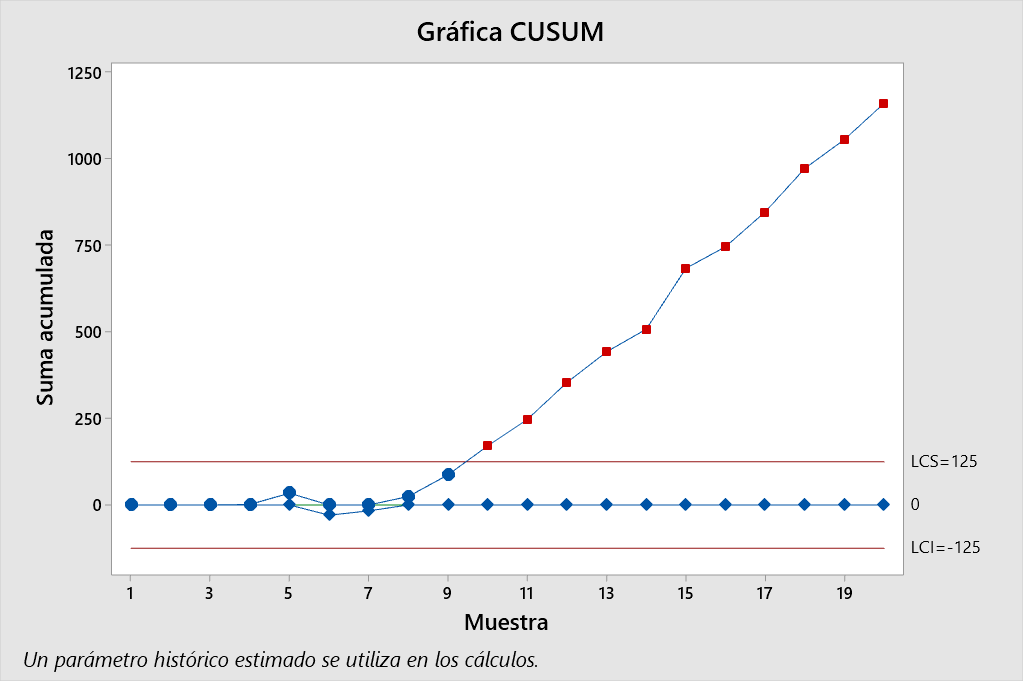
Los cálculos realizados muestran que el CUSUM superior en el período \(10\) es \(C_{10}^{+} = 170.5\). Como este es el primer período en el que \(C_{i}^{+}>H = 125\), concluyendo que el proceso está fuera de control en ese punto. El CUSUM tabular también indica cuándo probablemente ocurrió el cambio. El contador \(N^{+}\) registra el número de períodos consecutivos desde que el CUSUM \(C_{i}^{+}\) del lado superior se elevó por encima del valor de cero. Como \(N^{+}=3\) en el período \(10\), concluiríamos que el proceso tuvo el último control en el período \(10-3=7\), por lo que el cambio en la media del proceso probablemente ocurrió después de la observación número \(7\), entre los períodos \(7\) y \(8\).
En resumen, el proceso está fuera de control en la parte superior después de la observación \(7\).
- b). ¿Es razonable la estimación de \(\sigma\) utilizada en el apartado a). de este problema?
Data <- c(1045,1055,1037,1064,1095,1008,1050,1087,1125,1146,
1139,1169,1151,1128,1238,1125,1163,1188,1146,1167) %>% as.data.frame()
Rangos <- NULL; x <- Data
for (i in 1:(nrow(Data)-1)) {
Rangos[i+1] <- abs(x[i,1] - x[i+1,1])
}
# --------------------- Tabla de Control de Rango Móvil ---------------------- #
TCRM <- as.data.frame(cbind(x, "MR" = Rangos)) # MR: Moving Range
sum(TCRM$MR, na.rm = TRUE)
# [1] 738
d2_n1 <- 1.128
( MR_bar <- mean(TCRM$MR, na.rm = TRUE) )
# [1] 38.84211
( sigmaEst <- MR_bar/d2_n1 )
# [1] 34.43449\[\begin{align*} \overline{MR} &= \frac{1}{m-1}\sum_{i=1}^{m-1}R_i = \frac{738}{20-1} = 38.84211 \\ \widehat{\sigma} &= \frac{\overline{MR}}{d_2} = \frac{38.84211}{1.128} = 34.43449 \end{align*}\]
No parece razonable usar la estimación de \(\sigma\) (\(\widehat{\sigma}=25\)), dada en el apartado a)., para este problema ya que la estimación utilizada para \(\sigma\) es mucho menor que la varianza estimada por rangos móviles para dichas observaciones individuales, cuyo valor es igual a \(\widehat{\sigma}=34.43\).
8.8
Las concentraciones de baño se miden cada hora en un proceso químico. Los datos (en ppm) de las últimas 32 horas se muestran aquí (leer hacia abajo desde la izquierda). El objetivo del proceso es \(\mu_0 = 175\) ppm.
| 160 | 186 | 190 | 206 |
| 158 | 195 | 189 | 210 |
| 150 | 179 | 185 | 216 |
| 151 | 184 | 182 | 212 |
| 153 | 175 | 181 | 211 |
| 154 | 192 | 180 | 202 |
| 158 | 186 | 183 | 205 |
| 162 | 197 | 186 | 197 |
- a). Estime la desviación estándar del proceso.
Data <- c(160,158,150,151,153,154,158,162,186,195,179,184,175,192,186,197,
190,189,185,182,181,180,183,186,206,210,216,212,211,202,205,197) %>% as.data.frame()
Rangos <- NULL; x <- Data
for (i in 1:(nrow(Data)-1)) {
Rangos[i+1] <- abs(x[i,1] - x[i+1,1])
}
# --------------------- Tabla de Control de Rango Móvil ---------------------- #
TCRM <- as.data.frame(cbind(x, "MR" = Rangos)) # MR: Moving Range
sum(TCRM$MR, na.rm = T)
# [1] 197
d2_n1 <- 1.128
( MR_bar <- mean(TCRM$MR, na.rm = T) )
# [1] 6.354839
( sigmaEst <- MR_bar/d2_n1 )
# [1] 5.633722La estimación de la desviación estándar de un proceso con observaciones individuales se hace a partir del promedio de los rangos móviles de los datos. El vector \(MR\) es,
\[MR = (2 \,\, 8 \,\, 1 \,\, 2 \,\, 1 \,\, 4 \,\, 4 \,\, 24 \,\, 9 \,\, 16 \,\, 5 \,\, 9 \,\, 17 \,\, 6 \,\, 11 \,\, 7 \,\, 1 \,\, 4 \,\, 3 \,\, 1 \,\, 1 \,\, 3 \,\, 3 \,\, 20 \,\, 4 \,\, 6 \,\, 4 \,\, 1 \,\, 9 \,\, 3 \,\, 8)^t\]
Procederemos a calcular el promedio de este vector (\(\widehat{MR}\)), y ya teniendo esta información presente el estimador de sigma se define como \(\frac{\overline{MR}}{d_2}\), donde \(d_2=1.128\), con lo cual obtenemos que,
\[\begin{align*} \overline{MR} &= \frac{1}{m-1}\sum_{i=1}^{m-1}R_i = \frac{197}{32-1} = 6.3548 \\ \hat{\sigma} &= \frac{\overline{MR}}{d_2} = \frac{6.3548}{1.128} = 5.6337 \end{align*}\]
- b). Construya un CUSUM tabular para este proceso utilizando valores estandarizados de \(h = 5\) y \(k = \frac{1}{2}\).
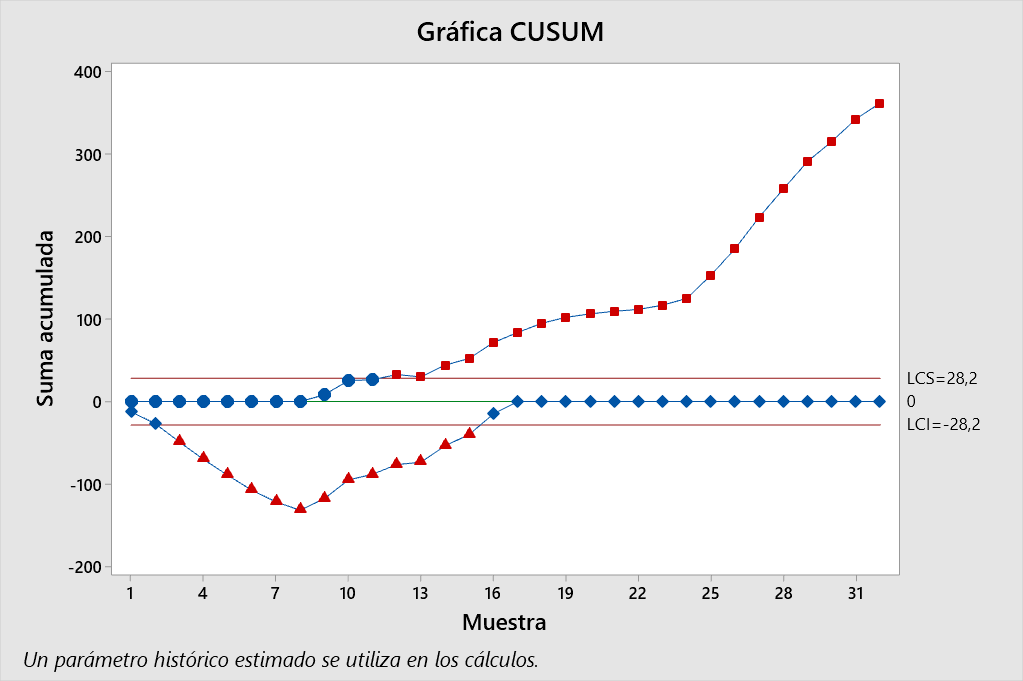
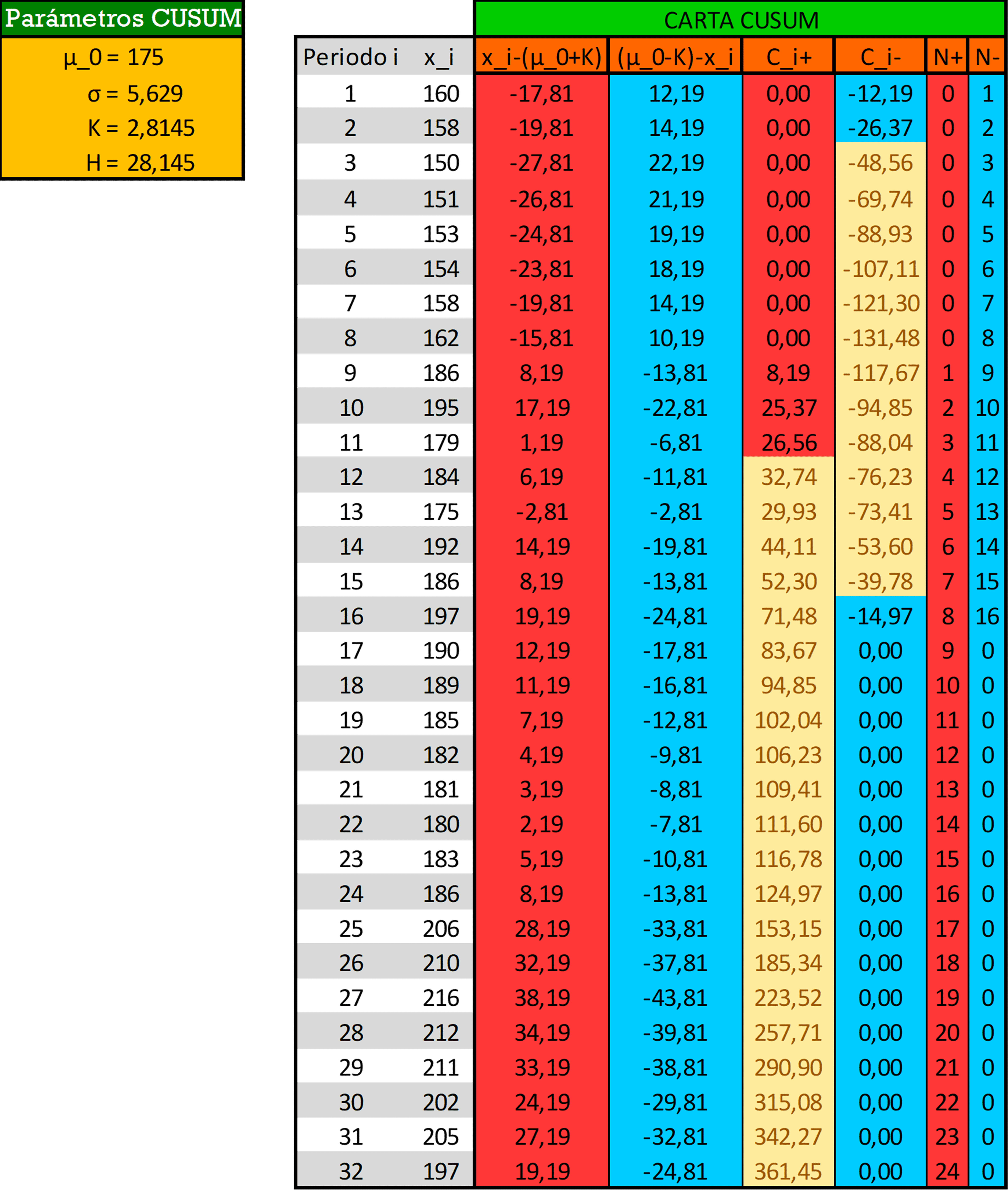
Se puede observar con claridad que el proceso está fuera de control desde la segunda observación de éste. Para ser más precisos se puede observar que en la primera parte del proceso la media disminuye de manera significante hasta la octava observación. A partir de este punto y hasta el final del proceso la media aumenta constantemente y se mantiene fuera de control.
En resumen, el proceso señala que se salió de control por debajo del \(LCI\) en la muestra número 3 y arriba del del \(LCS\) en la muestra número 12. Las causas asignables ocurrieron después del inicio (muestra \(3-3=0\)) y después de la muestra 8 (\(12-4\)).
8.15
Vuelva a realizar el ejercicio 8.1 utilizando un gráfico de control EWMA con \(\lambda = 0.1\) y \(L = 2.7\). Compare sus resultados con los obtenidos con la CUSUM.
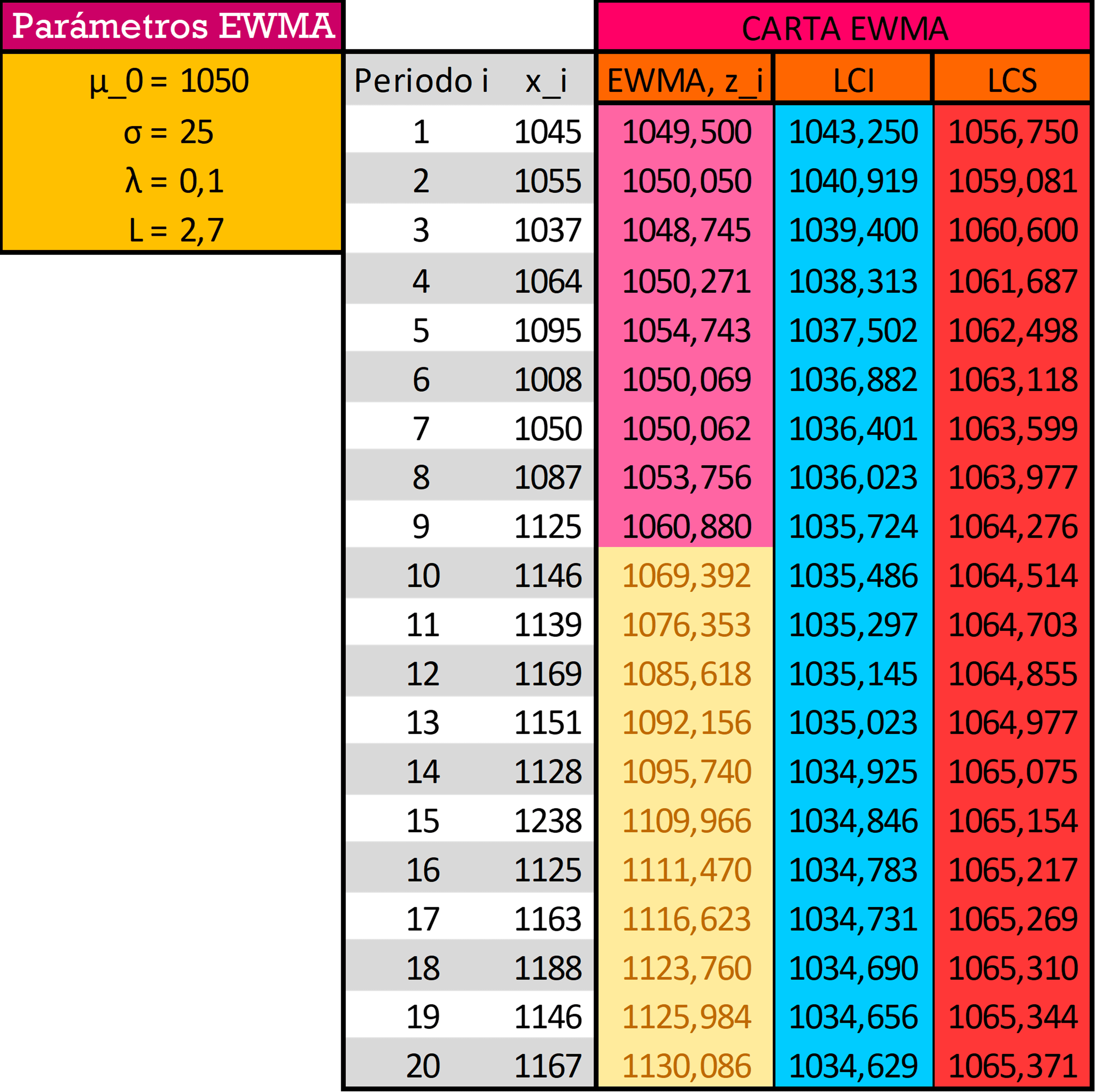
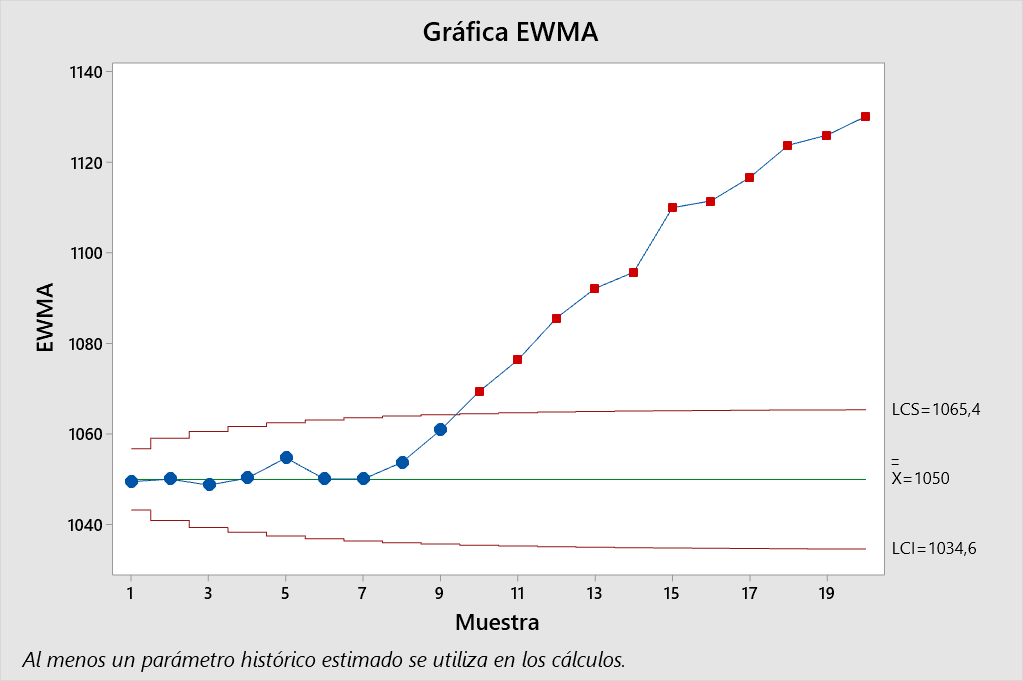
La carta EWMA queda definida por los límites,
\[\begin{align*} LCS &= \mu_0 + L\sigma \sqrt{\frac{\lambda}{2-\lambda}} = 1050 + 2.7\cdot 25\sqrt{\frac{0.1}{2-0.1}} = \color{red} {1065.486} \\ LC &= \mu_0 = \color{green} {1050} \\ LCI &= \mu_0 - L\sigma \sqrt{\frac{\lambda}{2-\lambda}} = 1050 - 2.7\cdot 25\sqrt{\frac{0.1}{2-0.1}} = \color{cyan} {1034.514} \end{align*}\]
El gráfico de control de EWMA señala que en la observación número \(10\) el proceso excede el límite de control superior (igual que la carta CUSUM). Esto muestra que la media incrementa significativamente durante el proceso. Ambas cartas tienen resultados muy similares al advertir sobre el incremento de la media desde la misma observación, y esto se debe en gran medida a que \(\lambda\) tiene un valor cercano a \(0\).
8.21
Reconsidere los datos en el ejercicio 8.8. Configure y aplique un gráfico de control EWMA a estos datos usando \(\lambda = 0.05\) y \(L = 2.6\).
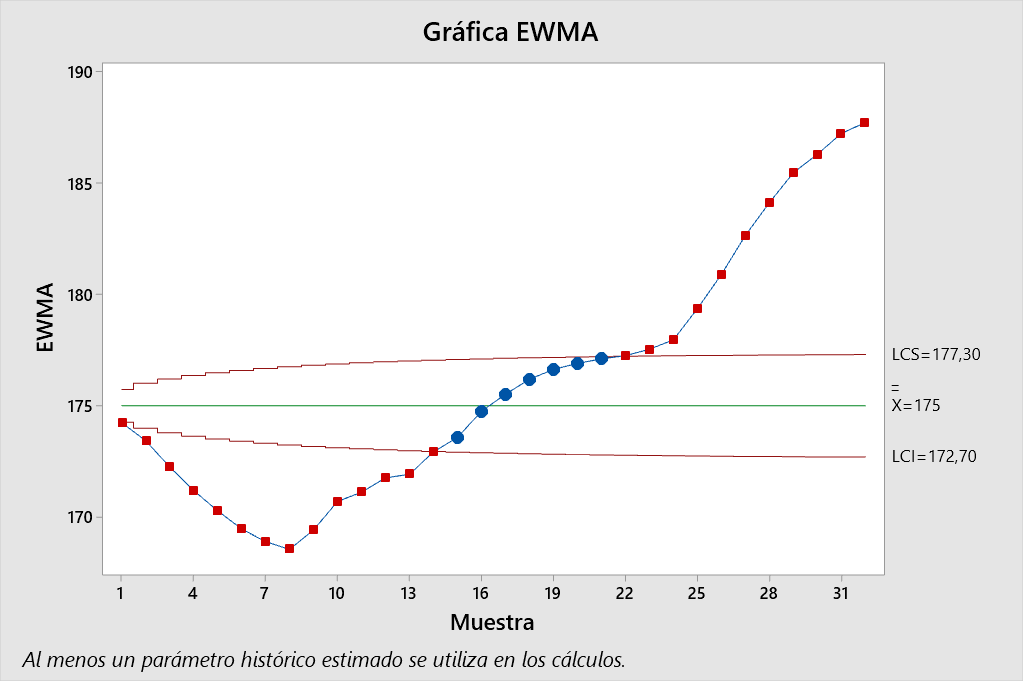
La carta EWMA queda definida por los límites,
\[\begin{align*} LCS &= \mu_0 + L\sigma \sqrt{\frac{\lambda}{2-\lambda}} = 175 + 2.6\cdot 5.6337\sqrt{\frac{0.05}{2-0.05}} = \color{red} {177.3455} \\ LC &= \mu_0 = \color{orange} {175} \\ LCI &= \mu_0 - L\sigma \sqrt{\frac{\lambda}{2-\lambda}} = 175 - 2.6\cdot 5.6337\sqrt{\frac{0.05}{2-0.05}} = \color{cyan} {172.6545} \end{align*}\]
Se puede observar que la carta EWMA muestra un proceso fuera de control. De hecho, esta carta entrega unos resultados muy similares a los de la carta CUSUM en términos de la falta de control. Esto se debe a que \(\lambda\) tiene un valor muy cercano a \(0\), por lo cual se les da poco peso a las observaciones recientes. Sin embargo, a diferencia de la carta CUSUM, en la carta EWMA no hay cambios drásticos entre dos observaciones consecutivas, sino cambios moderados también por este valor de \(\lambda\).
Ejercicios Propuestos por el Docente
1). Simulación de una carta CRL (ó CCC)
Construya una carta CRL (ó CCC) para \(p=0.02\) y \(\alpha=0.05\). Simule varios puntos y grafique la carta.
A continuación, simularemos la carta CRL para unidades producidas entre unidades defectuosas. Su utilidad radica cuando los defectos o defectos son raros y los subgrupos son pequeños, los gráficos C, U y P se vuelven inútiles, ya que la mayoría de los subgrupos no tendrán defectos. La distribución geométrica modela el número de unidades entre defectos.
set.seed(122333)
p <- 0.02
alpha <- 0.05 # Probabilidad de que la carta señale una falsa alarma
L <- (log(1-alpha))/(log(1-p))
mu <- 1/p
CRLs <- rgeom(n = 50, prob = p); n <- 1:length(CRLs)
plot(n, CRLs, type = "l", las = 1, main = "CARTA CRL/CCC",
sub = "# de artículos hasta obtener uno no conforme")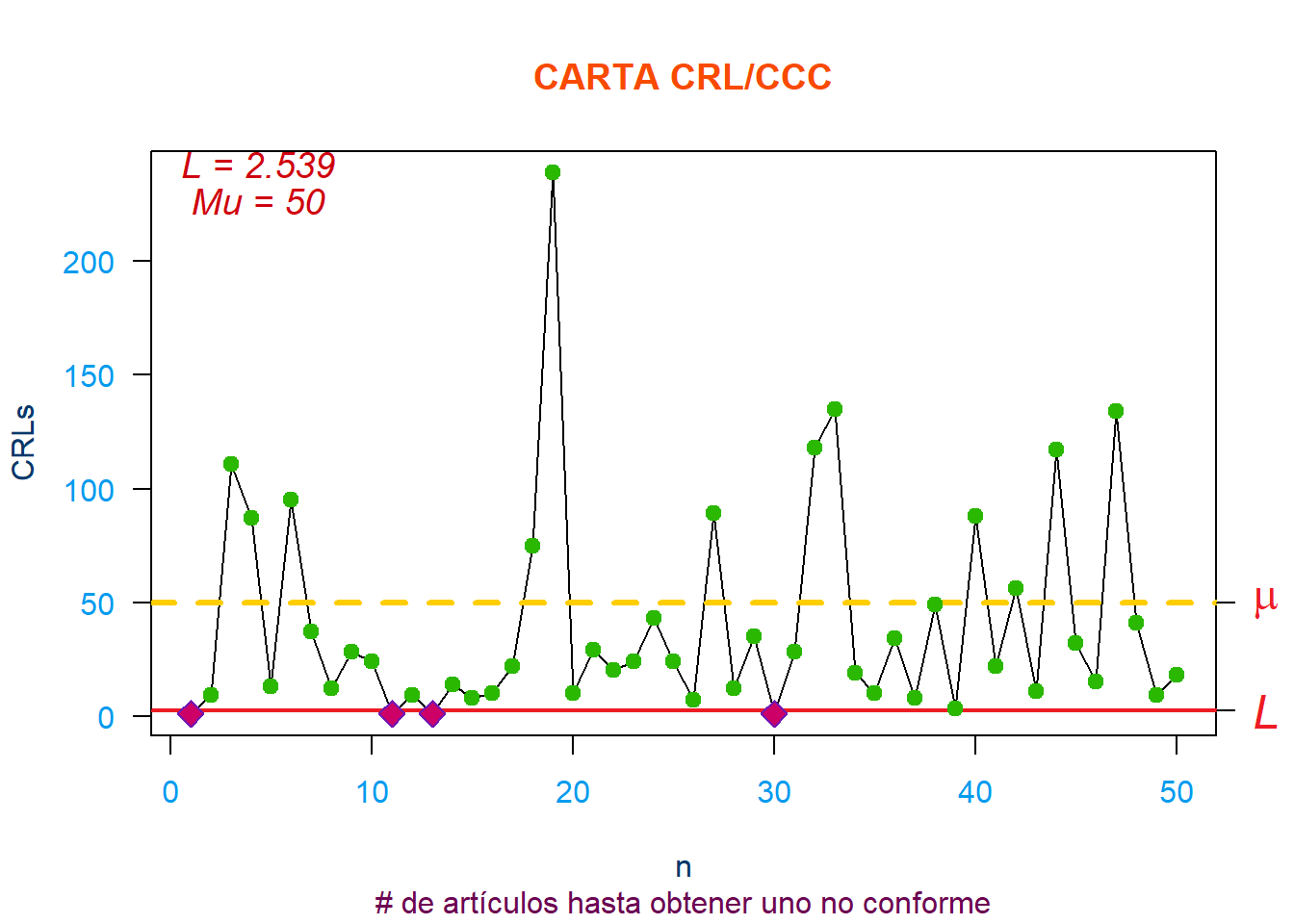
2). Comparación de las cartas Shewhart, CUSUM y EWMA para monitorear la media de un proceso
Genere 10 observaciones de una \(\mathcal{N}(\mu=0, \sigma^2=1)\). A partir de la observación \(11\) genere observaciones de una \(\mathcal{N}(\mu_1, 1)\) hasta que la carta produzca una señal.
Construir las tres cartas para, \[\mu_1 = \mu_0 + \delta\sigma_0\] donde \(\mu_0=0\) y \(\delta = 0.5, 1.0, 1.5, 2.0\) y \(2.5\)
Repita este proceso \(n\) veces (\(n=1.000\) o \(n=5.000\)) y calcule la \(ARL_1\). Obtenga conclusiones.
ARL_SHEWHART <- NULL ;ARL_CUSUM <- NULL; ARL_EWMA <- NULL
for (i in 1:10000) {
NumSample <- 10
mu0 <- 0; sigma <- 1
Muestras <- matrix(data = rnorm(NumSample, mu0, sigma), nrow = NumSample, ncol = 1)
# PARÁMETROS CARTA SHEWHART
L = 3
# PARÁMETROS CARTA CUSUM (valores de k y h que dan ARL0 = 370)
K = 0.25; H = 8.01
# PARÁMETROS CARTA EWMA (valores de Lambda y L que dan ARL0 = 370)
Lambda = 0.2; L_EWMA = 2.8593
# CARTAS
Carta_SHEWHART <- qcc(Muestras, type = "xbar.one", center = mu0,
limits = c(mu0-L*sigma,mu0+L*sigma), plot = FALSE)
Carta_CUSUM <- cusum(Muestras, center = mu0, std.dev = sigma,
decision.interval = H, se.shift = K, plot = FALSE)
Carta_EWMA <- ewma(Muestras, center = mu0, std.dev = sigma,
lambda = Lambda, nsigmas = L_EWMA, plot = FALSE)
# CAMBIO DE mu0
delta <- 0.0 # luego con c(0.0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0)
mu1 <- mu0 + (delta*sigma)
Muestras_SHEWHART = Muestras; Muestras_CUSUM = Muestras; Muestras_EWMA = Muestras
#===================================CARTA SHEWHART====================================#
Prueba_SHEWHART <- sum(Carta_SHEWHART$violations$beyond.limits)
while (Prueba_SHEWHART==0) {
x <- rnorm(n = 1, mean = mu1, sd = sigma)
Muestras_SHEWHART <- rbind(Muestras_SHEWHART, x)
rownames(Muestras_SHEWHART) <- 1:nrow(Muestras_SHEWHART)
Carta_SHEWHART <- qcc(Muestras_SHEWHART, type = "xbar.one", center = mu0,
limits = c(mu0-L*sigma,mu0+L*sigma), plot = FALSE)
Prueba_SHEWHART <- sum(Carta_SHEWHART$violations$beyond.limits)
}
ARL_SHEWHART[i] <- nrow(Muestras_SHEWHART)
#=====================================CARTA CUSUM=====================================#
Prueba_CUSUM <- sum(Carta_CUSUM$violations$upper)+sum(Carta_CUSUM$violations$lower)
while (Prueba_CUSUM==0) {
x <- rnorm(n = 1, mean = mu1, sd = sigma)
Muestras_CUSUM <- rbind(Muestras_CUSUM, x)
rownames(Muestras_CUSUM) <- 1:nrow(Muestras_CUSUM)
Carta_CUSUM <- cusum(Muestras_CUSUM, center = mu0, std.dev = sigma,
decision.interval = H, se.shift = K, plot = FALSE)
Prueba_CUSUM <- sum(Carta_CUSUM$violations$upper)+sum(Carta_CUSUM$violations$lower)
}
ARL_CUSUM[i] <- nrow(Muestras_CUSUM)
#=====================================CARTA EWMA======================================#
Prueba_EWMA <- sum(Carta_EWMA$violations)
while (Prueba_EWMA==0) {
x <- rnorm(n = 1, mean = mu1, sd = sigma)
Muestras_EWMA <- rbind(Muestras_EWMA, x)
rownames(Muestras_EWMA) <- 1:nrow(Muestras_EWMA)
Carta_EWMA <- ewma(Muestras_EWMA, center = mu0, std.dev = sigma,
lambda = Lambda, nsigmas = L_EWMA, plot = FALSE)
Prueba_EWMA <- sum(Carta_EWMA$violations)
}
ARL_EWMA[i] <- nrow(Muestras_EWMA)
}
( ARL1_SHEWHART <- mean(ARL_SHEWHART) )
( ARL1_CUSUM <- mean(ARL_CUSUM) )
( ARL1_EWMA <- mean(ARL_EWMA) )| No. Observación | \(x\) | No. Observación | \(x\) |
|---|---|---|---|
| 1 | 1045 | 11 | 1139 |
| 2 | 1055 | 12 | 1169 |
| 3 | 1037 | 13 | 1151 |
| 4 | 1064 | 14 | 1128 |
| 5 | 1095 | 15 | 1238 |
| 6 | 1008 | 16 | 1125 |
| 7 | 1050 | 17 | 1163 |
| 8 | 1087 | 18 | 1188 |
| 9 | 1125 | 19 | 1146 |
| 10 | 1146 | 20 | 1167 |
En la Tabla () se recogen algunos valores que permiten comparar la sensibilidad de las cartas Shewhart, CUSUM y EWMA. Primero fijamos el \(ARL_0\) de las tres cartas en \(370\) (eligiendo para ello los parámetros correspondientes que den dicho resultado, expuestos en la Figura al final del documento) para que así las cartas sean comparables, ya que un gráfico de control del tipo Shewhart con límites \(3\sigma\) viene a tener un \(ARL_0\) (bajo control) de 370 unidades.
En dicha tabla también podemos ver que el \(ARL_1\) para una carta Shewhart cuando la media se ha desplazado del promedio bajo control para \(\delta\leq 2.0\) es mucho mayor que en las cartas CUSUM y EWMA. Por lo tanto, se necesitarán menos muestras, en promedio, para detectar un cambio en la media con un punto fuera de los límites de control cuando se usan las cartas CUSUM y EWMA. Lo cual es precisamente la razón y utilidad de ellas.
Además, las cartas CUSUM y EWMA son mucho más sensible que la carta Shewhart para detectar variaciones pequeñas en la media. Para las variaciones grandes (\(\delta> 2.0\)) ambas cartas son similares e incluso peores a la de Shewhart. Finalmente, la eficiencia de estos gráficos también puede incrementarse mediante el cambio de sus parámetros, obteniendo que tanto la carta CUSUM como la EWMA sean capaces de detectar cambios “muy pequeños” en la media del proceso. Cabe resaltar que la carta de control EWMA es muy flexible y puede detectar tanto cambios grandes y pequeños en la media.

SOLUCIÓN TALLER #3
Exercises Introduction to Statistical Quality Control Montgomery
10.2
Un producto tiene tres características de calidad. Los valores nominales de estas características de calidad y su matriz de covarianza de muestra se han determinado a partir del análisis de \(30\) muestras preliminares de tamaño \(n=10\) de la siguiente manera:
\[ \overline{\overline{\textbf{x}}} = \begin{bmatrix} 3.0 \\ 3.5 \\ 2.8 \end{bmatrix} \hspace{0.5cm} \textbf{S} = \begin{bmatrix} 1.40 & 1.02 & 1.05 \\ 1.02 & 1.35 & 0.98 \\ 1.05 & 0.98 & 1.20 \end{bmatrix} \]
A continuación, se muestran las medias de muestra para cada característica de calidad para \(15\) muestras adicionales de tamaño \(n=10\). ¿Está el proceso en control estadístico?
| N | \(\overline{x}_1\) | \(\overline{x}_2\) | \(\overline{x}_3\) |
|---|---|---|---|
| 1 | 3.10 | 3.70 | 3.00 |
| 2 | 3.30 | 3.90 | 3.10 |
| 3 | 2.60 | 3.00 | 2.40 |
| 4 | 2.80 | 3.00 | 2.50 |
| 5 | 3.00 | 3.30 | 2.80 |
| 6 | 4.00 | 4.60 | 3.50 |
| 7 | 3.80 | 4.20 | 3.00 |
| 8 | 3.00 | 3.30 | 2.70 |
| 9 | 2.40 | 3.00 | 2.20 |
| 10 | 2.00 | 2.60 | 1.80 |
| 11 | 3.20 | 3.90 | 3.00 |
| 12 | 3.70 | 4.00 | 3.00 |
| 13 | 4.10 | 4.70 | 3.20 |
| 14 | 3.80 | 4.00 | 2.90 |
| 15 | 3.20 | 3.60 | 2.80 |
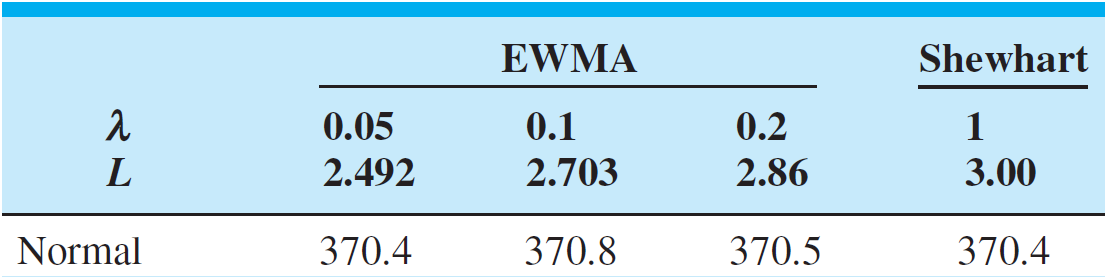
Los límites de control en Fase II, para la carta \(T^2\), con \(m=30\) muestras preliminares, \(n=10\) como tamaño de muestra, \(p=3\) características y con un \(\alpha=0.001\), es,
\[\begin{align*} LCS_{\text{Fase II}} &= \frac{p(m+1)(n-1)}{m(n-1)-p+1} F_{(\alpha, \,\,p, \,\,m(n-1)-p+1)} \\ &= \frac{3(30+1)(10-1)}{30(10-1)-3+1} F_{(0.001, \,\,3, \,\,30(10-1)-3+1)} \\ &= \frac{837}{268} F_{(0.001, \,\,3, \,\,268)} \\ &= \color{red} {17.425} \\ LCI_{\text{Fase II}} &= \color{cyan} {0} \end{align*}\]
De acuerdo con lo anterior, el proceso se encuentra fuera de control, debido a la muestra \(\#13\).
10.3
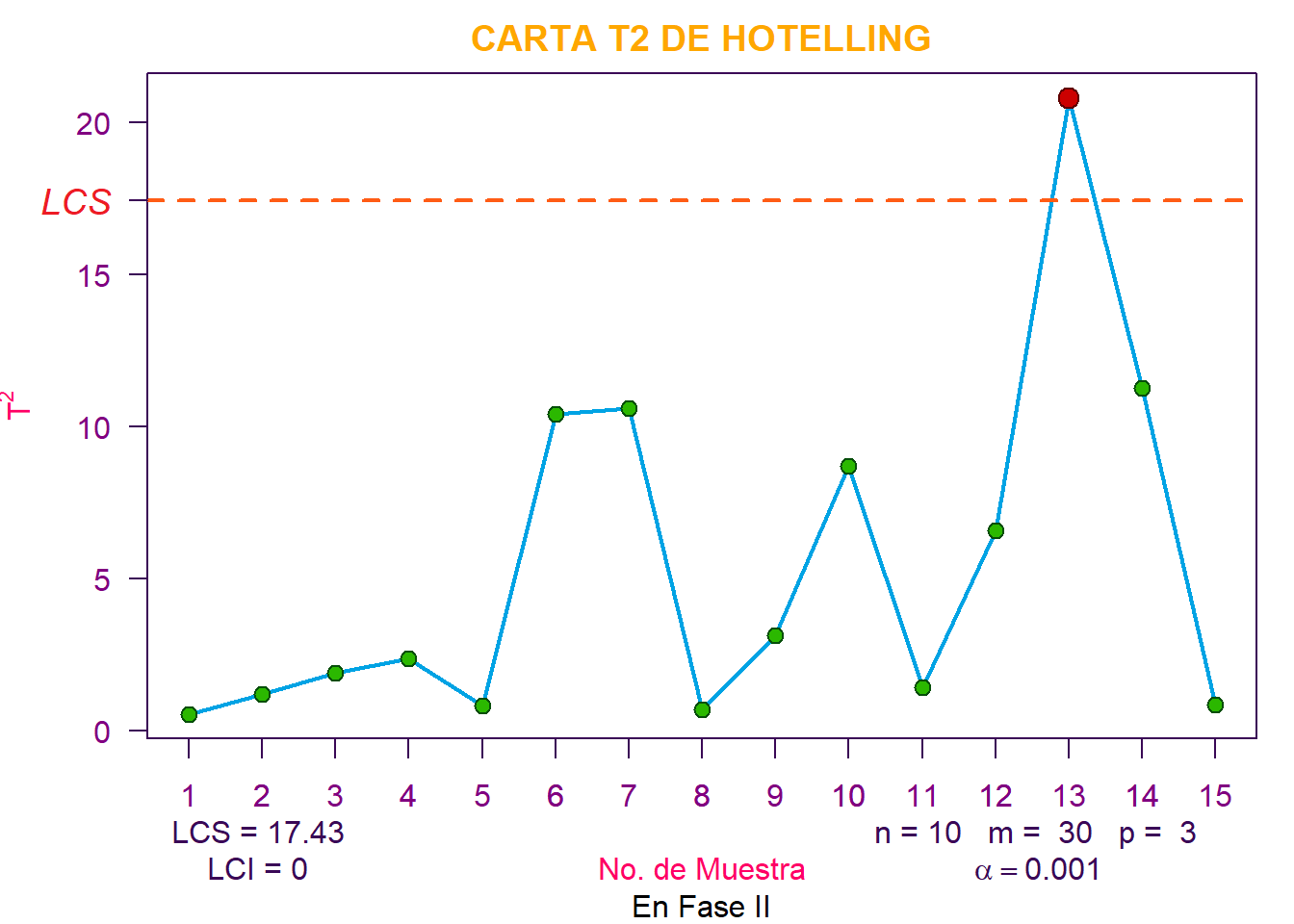
Reconsidere la situación en el ejercicio 10.1. Suponga que el vector de media muestral y la matriz de covarianza muestral provistos fueron los parámetros de la población real. ¿Qué límite de control sería apropiado para la Fase II para la tabla de control? Aplique este límite a los datos y discuta cualquier diferencia en los resultados que encuentre en comparación con la elección original del límite de control.
\[ \vec{\boldsymbol{\mu}}_0 = \begin{bmatrix} 55 \\ 30 \end{bmatrix} \hspace{0.5cm} \boldsymbol{\Sigma} = \begin{bmatrix} 200 & 130 \\ 130 & 120 \end{bmatrix} \]
Como los , se prosigue a construir el límite de control superior definido por,
\[LCS= \chi^2_{(\alpha, \,\,p)} = \chi^2_{(0.001, \,\,2)} = \color{magenta} {13.81551}\]
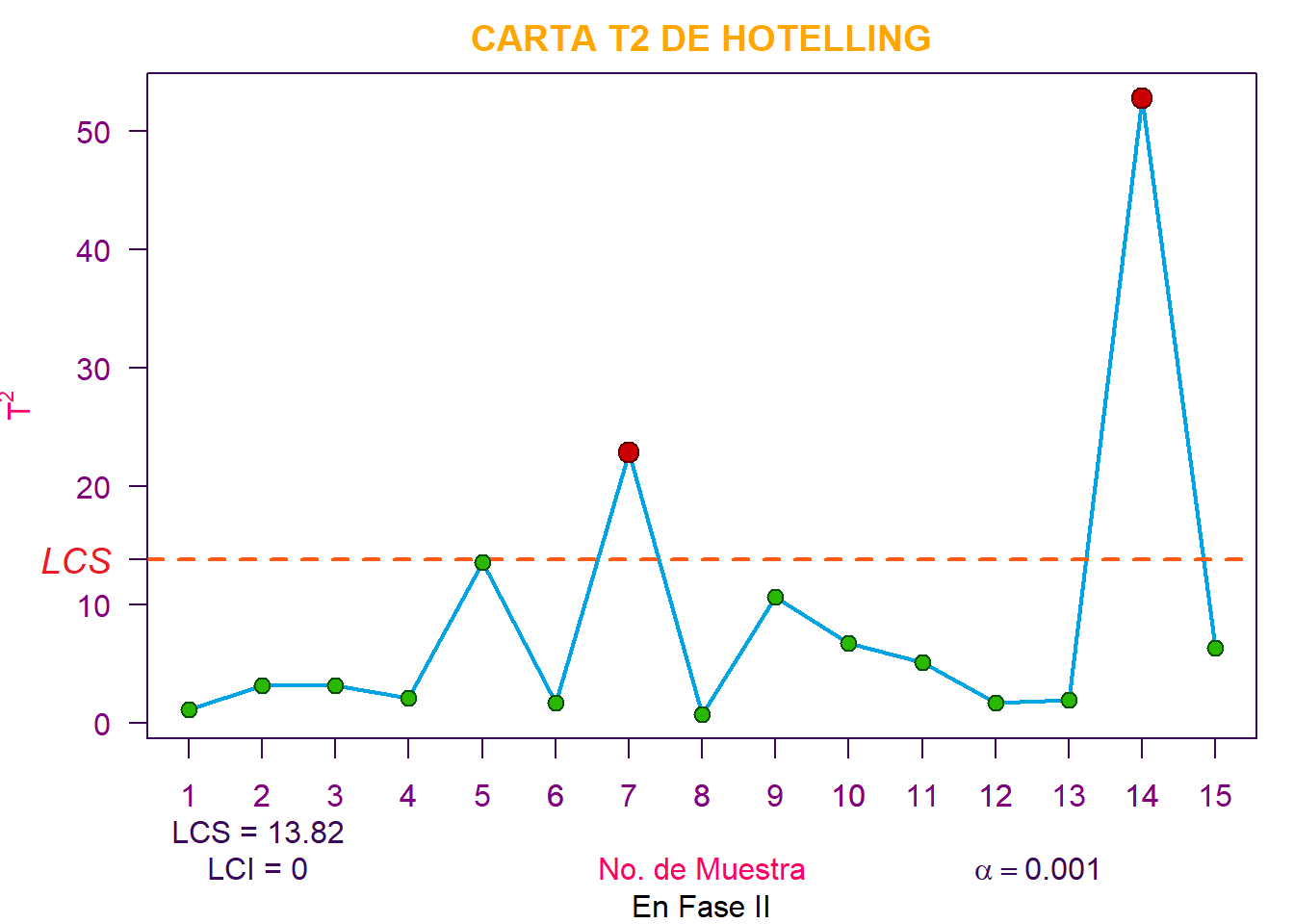
De acuerdo con lo anterior, el proceso está fuera de control en las muestras \(\#7\) y \(\#14\). Finalmente, podemos observar que se llegó a los mismos resultados del punto 10.1, en los que se usó los parámetros estimados a partir de las muestras (\(\overline{\overline{\textbf{x}}} \text{ y }\textbf{S}\)), y se obtuvo como \(LCS_{\text{Fase II}}=14.168\), el cual es mayor al que obtuvimos con la distribución \(\chi^2\).
\[\begin{align*} LCS_{\text{Fase II}} &= \frac{p(m+1)(n-1)}{m(n-1)-p+1} F_{(\alpha, \,\,p, \,\,m(n-1)-p+1)} \\ &= \frac{2(50+1)(25-1)}{50(25-1)-2+1} F_{(0.001, \,\,2, \,\,1199)}) \\ &= \color{purple} {14.18514} \end{align*}\]
Por lo que se puede decir que la suposición de que el vector de medias muestral y la matriz de covarianzas son realmente los parámetros poblacionales es parcialmente correcta ya que el resultado es el mismo.
10.5
Considere una carta de control \(T^2\) para monitorear \(p=6\) características de calidad. Suponga que el tamaño del subgrupo es \(n=3\) y que hay \(30\) muestras preliminares disponibles para estimar la matriz de covarianza de la muestra.
- a). Encuentre los límites de control de la Fase II suponiendo que \(\alpha = 0.005\).
\[\begin{align*} LCS_{\text{Fase II}} &= \frac{p(m+1)(n-1)}{m(n-1)-p+1} F_{(\alpha, \,\,p, \,\,m(n-1)-p+1)} \\ &= \frac{6(30+1)(3-1)}{30(3-1)-6+1} F_{(0.005, \,\,6, \,\,30(3-1)-6+1}) \\ &= \frac{372}{55} F_{(0.005, \,\,6, \,\,55)} \\ &= \color{red} {23.882} \\ LCI_{\text{Fase II}} &= \color{cyan} {0} \end{align*}\]
alpha <- 0.005
p <- 6; m <- 30; n <- 3
Quantil <- qf(alpha, p, m*(n-1)-p+1, lower.tail = FALSE)
LCS_FaseII <- ((p*(m+1)*(n-1)) / (m*(n-1)-p+1)) * Quantil
# [1] 23.88201- b). Compare los límites de control de la parte a). con el límite de control de chi-cuadrado. ¿Cuál es la magnitud de la diferencia en los dos límites de control?
\[\begin{align*} LCS_{\text{chi-cuadrado}} &= \chi^2_{(\alpha, \,\,p)} = \chi^2_{(0.005, \,\,6)} \\ &= \color{purple} {18.5476} \\ LCI_{\text{chi-cuadrado}} &= \color{magenta} {0} \end{align*}\]
LCS_chi <- qchisq(alpha, p, lower.tail = FALSE)
# [1] 18.54758Podemos observar que el \(LCS_{\text{Fase II}}\) es \(\approx 30\%\) (\(\frac{23.882}{18.5476} \cdot100\% = 128.76\%\)) más grande que el \(LCS_{\text{chi-cuadrado}}\).
- c). ¿Cuántas muestras preliminares tendrían que tomarse para asegurar que el límite de control exacto de la Fase II esté dentro del \(1\%\) del límite de control de chi-cuadrado?
Meta <- 1.01*LCS_chi
m <- seq(30, 800, by = 1)
Num <- NULL; Denom <- NULL; F <- NULL; LCS <- NULL
for (i in 1:length(m)) {
Num[i] <- p*(m[i]+1)*(n-1)
Denom[i] <- m[i]*(n-1)-p+1
F[i] <- qf(alpha, p, m[i]*(n-1)-p+1, lower.tail = FALSE)
LCS[i] <- (Num[i]/Denom[i])*F[i]
}
Matriz <- cbind(m, Num, Denom, F, LCS)
Matriz[Meta-Matriz[,5]>0, ][1:2,]## m Num Denom F LCS
## [1,] 719 8640 1433 3.106998 18.73305
## [2,] 720 8652 1435 3.106976 18.73279Deben tomarse \(m = 719\) muestras preliminares para garantizar que el límite exacto de la Fase II esté dentro del \(1\%\) del límite de chi-cuadrado.
10.7
Considere una tabla de control \(T^2\) para monitorear \(p=10\) características de calidad. Suponga que el tamaño del subgrupo es \(n=3\) y que hay \(25\) muestras preliminares disponibles para estimar la matriz de covarianza de la muestra.
- a). Encuentre los límites de control de la Fase II suponiendo que \(\alpha=0.005\).
\[\begin{align*} LCS_{\text{Fase II}} &= \frac{p(m+1)(n-1)}{m(n-1)-p+1} F_{(\alpha, \,\,p, \,\,m(n-1)-p+1)} \\ &= \frac{10(25+1)(3-1)}{25(3-1)-10+1} F_{(0.005, \,\,10, \,\,25(3-1)-10+1)} \\ &= \frac{520}{41} F_{(0.005, \,\,10, \,\,41)} \\ &= \color{red} {39.3261} \\ LCI_{\text{Fase II}} &= \color{cyan} {0} \end{align*}\]
alpha <- 0.005
p <- 10; m <- 25; n <- 3
Quantil <- qf(alpha, p, m*(n-1)-p+1, lower.tail = FALSE)
LCS_FaseII <- ((p*(m+1)*(n-1)) / (m*(n-1)-p+1)) * Quantil
# [1] 39.32609- b). Compare los límites de control de la parte a). con el límite de control de chi-cuadrado. ¿Cuál es la magnitud de la diferencia en los dos límites de control?
\[\begin{align*} LCS_{\text{chi-cuadrado}} &= \chi^2_{(\alpha, \,\,p)} = \chi^2_{(0.005, \,\,10)} \\ &= \color{red} {25.1882} \\ LCI_{\text{chi-cuadrado}} &= \color{cyan} {0} \end{align*}\]
LCS_chi <- qchisq(alpha, p, lower.tail = FALSE)
# [1] 25.18818Podemos observar que el \(LCS_{\text{Fase II}}\) es \(\approx 56\%\) (\(\frac{39.32609}{25.18818} \cdot100\% = 156.13%)\)) más grande que el \(LCS_{\text{chi-cuadrado}}\).
- c). ¿Cuántas muestras preliminares tendrían que tomarse para garantizar que el límite de control de chi-cuadrado esté dentro del \(1\%\) del límite de control exacto de la Fase II?
Meta <- 1.01*LCS_chi
m <- seq(25, 1000, by = 1)
Num <- NULL; Denom <- NULL; F <- NULL; LCS <- NULL
for (i in 1:length(m)) {
Num[i] <- p*(m[i]+1)*(n-1)
Denom[i] <- m[i]*(n-1)-p+1
F[i] <- qf(alpha, p, m[i]*(n-1)-p+1, lower.tail = FALSE)
LCS[i] <- (Num[i]/Denom[i])*F[i]
}
Matriz <- cbind(m, Num, Denom, F, LCS)
Matriz[Meta-Matriz[,5]>0, ][1:2,]## m Num Denom F LCS
## [1,] 988 19780 1967 2.529845 25.43992
## [2,] 989 19800 1969 2.529834 25.43967Deben tomarse \(m = 988\) muestras preliminares para garantizar que el límite exacto de la Fase II esté dentro del \(1\%\) del límite de chi-cuadrado.
10.11
Supongamos que tenemos características de calidad \(p = 3\), y en forma de correlación las tres variables tienen unidad de varianza y todos los coeficientes de correlación por pares son \(0.8\). El valor bajo control del vector medio del proceso es \(\vec{\boldsymbol{\mu}}' = [0, 0, 0]\).
- a). Escriba la matriz de covarianza \(\boldsymbol{\Sigma}\).
\[ \boldsymbol{\Sigma} = \begin{pmatrix} 1.0 & 0.8 & 0.8 \\ 0.8 & 1.0 & 0.8 \\ 0.8 & 0.8 & 1.0 \end{pmatrix} \]
- b). ¿Cuál es el límite de control de chi-cuadrado para el gráfico, suponiendo que \(\alpha=0.05\)?
\[\begin{align*} LCS_{\text{chi-cuadrado}} &= \chi^2_{(\alpha, \,\,p)} = \chi^2_{(0.05, \,\,3)} \\ &= \color{red} {7.8147} \\ LCI_{\text{chi-cuadrado}} &= \color{cyan} {0} \end{align*}\]
alpha <- 0.05; p <- 3
LCS <- qchisq(alpha, p, lower.tail = FALSE)
# [1] 7.814728- c). Suponga que una muestra de observaciones da como resultado el vector de observación estandarizado \(\vec{\textbf{y}}' = [1, 2, 0]\). Calcule el valor de la estadística \(T^2\). ¿Se genera una señal fuera de control?
y <- matrix(c(1, 2, 0), ncol = 1)
mu <- matrix(c(0, 0, 0), ncol = 1)
Sigma <- matrix(c(1.0, 0.8, 0.8,
0.8, 1.0, 0.8,
0.8, 0.8, 1.0), nrow = 3)
T2 <- t(y)%*%solve(Sigma)%*%y
# [1,] 11.15385De acuerdo con lo anterior, obtenemos que la estadística \(T^2 = 11.154\). Con lo cual, sí se genera una señal fuera de control, debido a que \(T^2 = 11.154 \color{green} {>} LCS_{\text{chi-cuadrado}} = 7.8147\).
- d). Calcule las cantidades de diagnóstico \(d_i\), \(i = 1,2,3\). ¿Ayuda esta información a identificar qué variables del proceso han cambiado?
\[d_i = T^2-T_{(i)}^2\]
Donde \(T_{(i)}\) es el valor de la estadística \(T^2\) para todas las observaciones del proceso exceptuando la i-ésima.
X2 <- qchisq(0.05, 1, lower.tail = FALSE)
T2 <- t(y)%*%solve(Sigma)%*%y
T2_i <- NULL; d <- NULL
for (i in 1:length(y)) {
T2_i[i] <- t(y[-i])%*%solve(Sigma[-i,-i])%*%y[-i]
d[i] <- T2-T2_i[i]
}
cbind("Variable" = 1:length(y), "T^2" = rep(T2,length(y)), "T^2_(i)" = T2_i, "d_i" = d, "Investigar" = d>X2)## Variable T^2 T^2_(i) d_i Investigar
## [1,] 1 11.15385 11.111111 0.04273504 0
## [2,] 2 11.15385 2.777778 8.37606838 1
## [3,] 3 11.15385 5.000000 6.15384615 1\[\begin{align*} d_1 &= T^2 - T^2_{(1)} = 11.154 - 11.111 = 0.043 \\ d_2 &= T^2 - T^2_{(2)} = 11.154 - 2.778 = 8.376 \\ d_3 &= T^2 - T^2_{(3)} = 11.154 - 5 = 6.154 \end{align*}\]
Para las variables \(\#2\) y \(\#3\) se observa que \(d_i \color{green}{ >} \chi^2_{(\alpha=0.05, \,\,1)} = 3.841\), por lo tanto, dichas variables contribuyen significativamente a la señal fuera de control y se deben investigar.
- e). Suponga que una muestra de observaciones da como resultado el vector de observación estandarizado \(\vec{\textbf{y}}' = [2, 2, 1]\). Calcule el valor de la estadística \(T^2\). ¿Se genera una señal fuera de control?
y <- matrix(c(2, 2, 1), ncol = 1)
T2 <- t(y)%*%solve(Sigma)%*%y
# [1,] 6.538462\[\begin{align*} T^2 = (x-\overline{x})^tS^{-1}(x-\overline{x}) = 6.5385 \end{align*}\]
De acuerdo con lo anterior, obtenemos que la estadística \(T^2 = 6.538\). Con lo cual, no se genera una señal fuera de control, debido a que \(T^2 = 6.538 \ngtr LCS_{\text{chi-cuadrado}} = 7.8147\).
- f). Para el caso en e)., calcule las cantidades de diagnóstico \(d_i\), \(i = 1,2,3\). ¿Ayuda esta información a identificar qué variables del proceso han cambiado?
X2 <- qchisq(0.05, 1, lower.tail = FALSE)
T2 <- t(y)%*%solve(Sigma)%*%y
T2_i <- NULL; d <- NULL
for (i in 1:length(y)) {
T2_i[i] <- t(y[-i])%*%solve(Sigma[-i,-i])%*%y[-i]
d[i] <- T2-T2_i[i]
}
cbind("Variable" = 1:length(y), "T^2" = rep(T2,length(y)), "T^2_(i)" = T2_i, "d_i" = d, "Investigar" = d>X2)## Variable T^2 T^2_(i) d_i Investigar
## [1,] 1 6.538462 5.000000 1.538462 0
## [2,] 2 6.538462 5.000000 1.538462 0
## [3,] 3 6.538462 4.444444 2.094017 0\[\begin{align*} d_1 &= T^2 - T^2_{(1)} = 6.5385 - 5 = 1.5385 \\ d_2 &= T^2 - T^2_{(2)} = 6.5385 - 5 = 1.5385 \\ d_3 &= T^2 - T^2_{(3)} = 6.5385 - 4.4444 = 2.094 \end{align*}\]
Como no se generó una señal fuera de control en e)., no es necesario calcular las cantidades de diagnóstico (\(d_i\)). Sin embargo, al realizarlas se confirma lo dicho anteriormente ya que ninguno de los \(d_i\) supera el límite de control (\(\chi^2_{(\alpha=0.05, \,\,1)} = 3.841\)).
Ejercicios Propuestos por el Docente
1). Considere los datos del problema 10.2
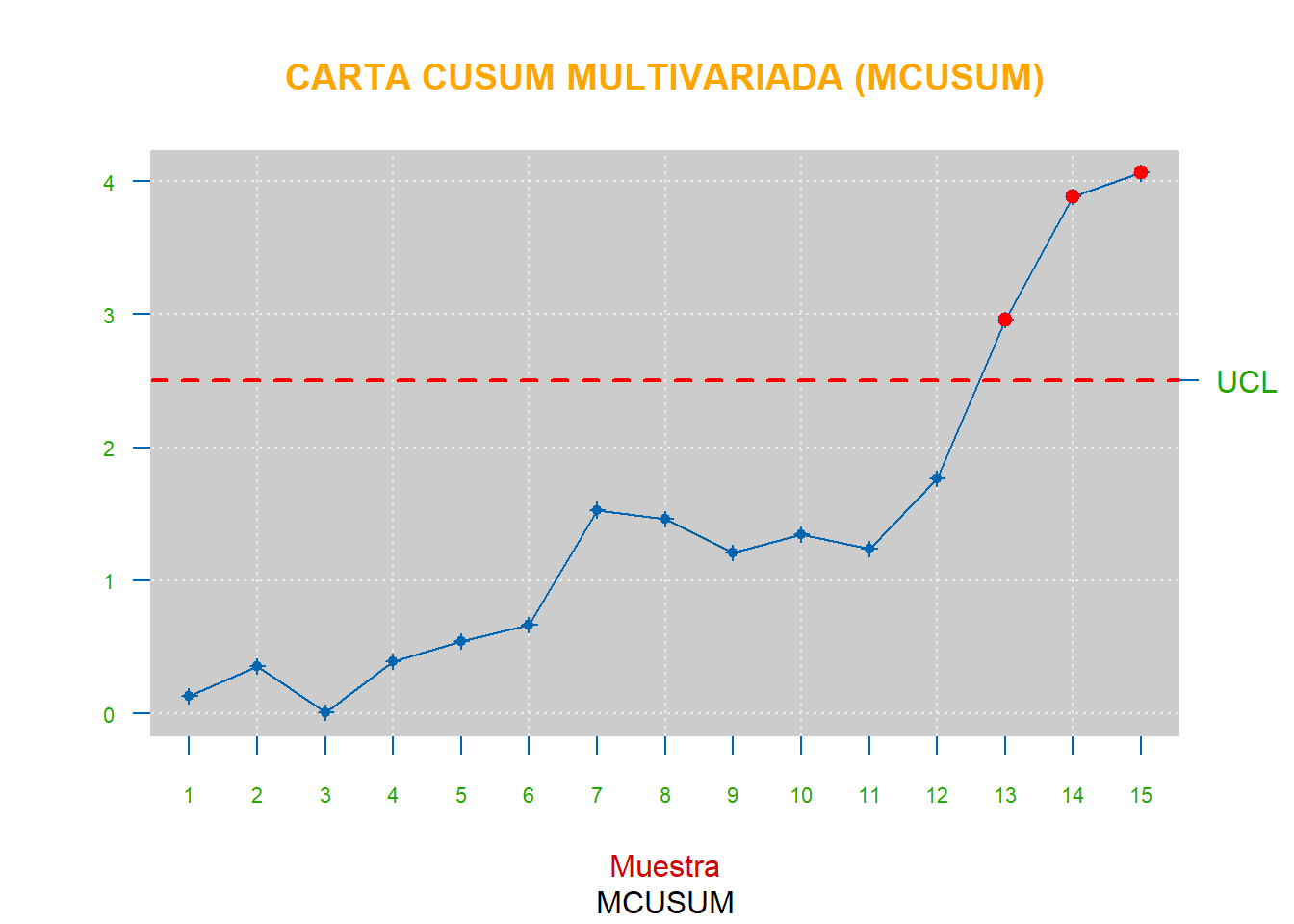
- a). Construya una carta MCUSUM
- b). Construya una carta MEWMA
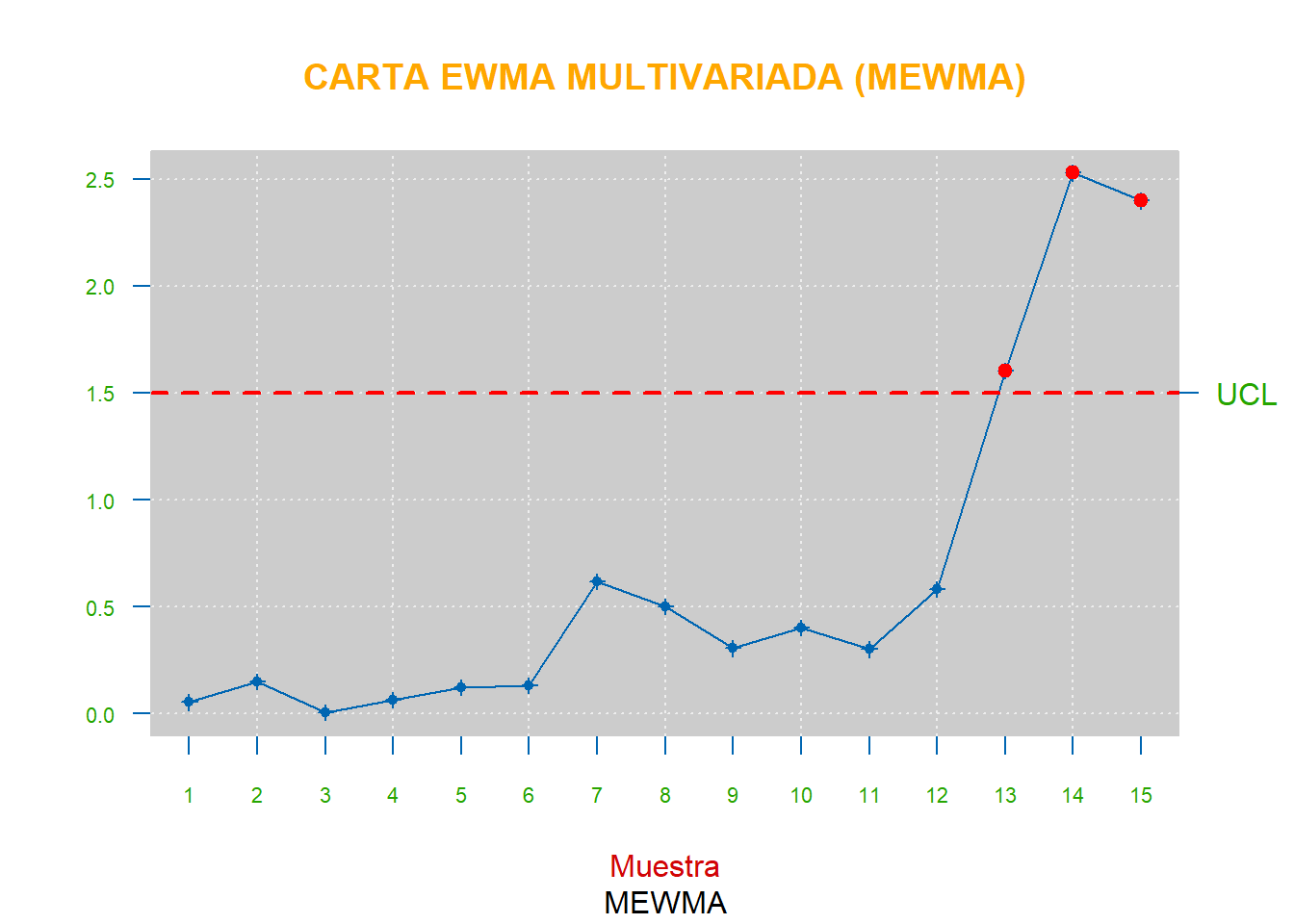
Después de realizar ambas cartas se puede observar un comportamiento similar entre ellas y que en ambas el proceso está fuera de control, al igual que cuando se realizó la carta \(T^2\) de Hotelling en el punto 10.2. Dicho resultado era de esperar, ya que las cartas MCUSUM y MEWMA son más sensibles a cambios en el vector de medias.
2). Comparación de las cartas \(T^2\) de Hotelling, MCUSUM y MEWMA para monitorear el vector de medias de un proceso multivariado
Asuma que el proceso bajo control sigue una distribución normal multivariada con \(\vec{\boldsymbol{\mu}}' = (0 \,\,0 \,\,0)'\) y
\[ \boldsymbol{\Sigma} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \]
Genere observaciones de una \(\mathcal{N}_3(\vec{\boldsymbol{\mu}}_1, \boldsymbol{\Sigma})\) y calcule el \(ARL_1\) para las tres cartas para varios valores de \(\vec{\boldsymbol{\mu}}_1\). Obtenga conclusiones.
Para el siguiente ejercicio de simulación vamos a considerar los siguientes valores de \(\delta\), con los que obtenemos un respetivo cambio para \(\vec{\boldsymbol{\mu}}_1\).
| \(\delta\) | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
|---|---|---|---|---|---|---|---|
| \(\vec{\boldsymbol{\mu}}_1'\) | \((0\,0\,0)'\) | \((0.5\,0.5\,0.5)'\) | \((1\,1\,1)'\) | \((1.5\,1.5\,1.5)'\) | \((2\,2\,2)'\) | \((2.5\,2.5\,2.5)'\) | \((3\,3\,3)'\) |
ARL_T2Hotelling <- NULL ;ARL_MCUSUM <- NULL; ARL_MEWMA <- NULL
for (i in 1:10000) {
mu0 <- matrix(c(0,0,0), ncol = 1)
Sigma <- diag(3)
Muestras <- rmvnorm(n = 20, mean = mu0, sigma = Sigma)
# PARÁMETROS CARTA T2 HOTELLING
Alpha = 0.001
# PARÁMETROS CARTA MCUSUM (valores de k y h que dan ARL0 = 200)
K = 0.5; h = 30.5
# PARÁMETROS CARTA MEWMA (valores de Lambda y H que dan ARL0 = 200)
Lambda = 0.5; p = 3
# delta <- sqrt( t(mu)%*%solve(Sigma)%*%mu )
H <- round(mewma.crit(l = Lambda, L0 = 200, p = p), 3)
# CARTAS
Carta_T2Hotelling <- mqcs.t2(Muestras, Xmv = mu0, S = Sigma, alpha = Alpha, phase = 2, plot = F)
Carta_MCUSUM <- mqcs.mcusum(Muestras, Xmv = mu0, S = Sigma, k = K, h = h, phase = 2, plot = F)
Carta_MEWMA <- mqcs.mewma(Muestras, limits = c(0,H), Xmv = mu0, S = Sigma, phase = 2, plot = F)
# CAMBIO DE mu0
delta <- 0.0 # Luego para 0.5, 1, 1.5, 2, 2.5 y 3
mu1 <- mu0 + delta
Muestras_T2Hotelling = Muestras; Muestras_MCUSUM = Muestras; Muestras_MEWMA = Muestras
#================================ CARTA T2 DE HOTELLING =================================#
Prueba_T2Hotelling <- sum(Carta_T2Hotelling$violations)
while (Prueba_T2Hotelling==0) {
x <- rmvnorm(n = 1, mean = mu1, sigma = Sigma)
Muestras_T2Hotelling <- rbind(Muestras_T2Hotelling, x)
rownames(Muestras_T2Hotelling) <- 1:nrow(Muestras_T2Hotelling)
Carta_T2Hotelling <- mqcs.t2(Muestras_T2Hotelling, Xmv = mu0, S = Sigma, alpha = Alpha, phase = 2, plot = F)
Prueba_T2Hotelling <- sum(Carta_T2Hotelling$violations)
}
ARL_T2Hotelling[i] <- nrow(Muestras_T2Hotelling)
#===================================== CARTA MCUSUM ====================================#
Prueba_MCUSUM <- sum(Carta_MCUSUM$violations)
while (Prueba_MCUSUM==0) {
x <- rmvnorm(n = 1, mean = mu1, sigma = Sigma)
Muestras_MCUSUM <- rbind(Muestras_MCUSUM, x)
rownames(Muestras_MCUSUM) <- 1:nrow(Muestras_MCUSUM)
Carta_MCUSUM <- mqcs.mcusum(Muestras_MCUSUM, Xmv = mu0, S = Sigma, k = K, h = h, phase = 2, plot = F)
(Prueba_MCUSUM <- sum(Carta_MCUSUM$violations))
}
ARL_MCUSUM[i] <- nrow(Muestras_MCUSUM)
#===================================== CARTA MEWMA =====================================#
Prueba_MEWMA <- sum(Carta_MEWMA$violations)
while (Prueba_MEWMA==0) {
x <- rmvnorm(n = 1, mean = mu1, sigma = Sigma)
Muestras_MEWMA <- rbind(Muestras_MEWMA, x)
rownames(Muestras_MEWMA) <- 1:nrow(Muestras_MEWMA)
Carta_MEWMA <- mqcs.mewma(Muestras_MEWMA, limits = c(0,H), Xmv = mu0, S = Sigma, phase = 2, plot = F)
Prueba_MEWMA <- sum(Carta_MEWMA$violations)
}
ARL_MEWMA[i] <- nrow(Muestras_MEWMA)
}
( ARL1_T2Hotelling <- mean(ARL_T2Hotelling) )
( ARL1_MCUSUM <- mean(ARL_MCUSUM) )
( ARL1_MEWMA <- mean(ARL_MEWMA) )| \(\delta\) | \(\textrm{ARL}_1T^2\) | \(\textrm{ARL}_1\textit{MCUSUM}\) | \(\textrm{ARL}_1\textit{MEWMA}\) |
|---|---|---|---|
| 0.0 | 200.8 | 199.5 | 199.2 |
| 0.5 | 130.02 | 32.7 | 31.8 |
| 1.0 | 52.64 | 11.3 | 11.1 |
| 1.5 | 20.48 | 6.69 | 6.47 |
| 2.0 | 8.82 | 4.86 | 4.7 |
| 2.5 | 4.34 | 3.83 | 3.79 |
| 3.0 | 2.55 | 3.2 | 3.17 |
La carta \(T^2\) de Hotelling, aunque es extremadamente eficaz, no es la única herramienta disponible para el análisis multivariante de procesos industriales. En algunos casos, otros tipos de gráficos de control multivariados pueden complementar o reemplazar este gráfico con mejores resultados.
Los gráficos MCUSUM y MEWMA son alternativas a la carta \(T^2\) de Hotelling en situaciones en las que es importante detectar pequeños cambios en los parámetros de un proceso. En tales situaciones, estos gráficos tienen un mejor rendimiento en términos de ARL y, por lo tanto, son más sensibles que la carta \(T^2\) de Hotelling para detectar un pequeño cambio en el vector de medias del proceso que permite una acción más rápida.
Cómo se puede ver en la Tabla (), al igual que en el caso univariado, la carta \(T^2\) de Hotelling es más sensible a cambios mayores en el vector de medias del proceso. Por otro lado, para pequeños cambios, los gráficos MCUSUM y MEWMA son más sensibles (cartas más potentes). Finalmente, podemos concluir que la diferencia existente entre el rendimiento de estas dos cartas {\(T^2\) de Hotelling vs. MCUSUM (Suma acumulativa multivariada) y MEWMA (Promedio móvil ponderado exponencial multivariante)} para esta situación (cuando \(p = 3\) variables) se considera significativa.
